题目内容
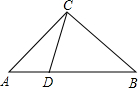 △ABC中,D为AB边上一点,∠ABC=∠ACD,且AC=6,BD=5,则AD=________.
△ABC中,D为AB边上一点,∠ABC=∠ACD,且AC=6,BD=5,则AD=________.
4
分析:由已知得∠ABC=∠ACD,加上角A是公共角,利用两角相等的两三角形相似得到三角形ADC与三角形ABC相似,然后根据相似三角形的对应边成比例,利用AC=6,BD=5,即可得到关于AD的一元二次方程,求出方程的解即可得到满足题意的AD的值.
解答:∵∠ABC=∠ACD,且∠A是公共角,
∴△ACD∽△ACB,
∴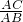 =
=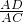 ,即AC2=AD(AD+DB)
,即AC2=AD(AD+DB)
∵AC=6,BD=5,
∴AD2+5AD-36=0,解得:AD=4,AD=-9(舍去),
∴AD=4.
故答案为:4.
点评:此题考查了相似三角形的判断与性质,是一道中档题.
分析:由已知得∠ABC=∠ACD,加上角A是公共角,利用两角相等的两三角形相似得到三角形ADC与三角形ABC相似,然后根据相似三角形的对应边成比例,利用AC=6,BD=5,即可得到关于AD的一元二次方程,求出方程的解即可得到满足题意的AD的值.
解答:∵∠ABC=∠ACD,且∠A是公共角,
∴△ACD∽△ACB,
∴
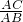 =
=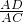 ,即AC2=AD(AD+DB)
,即AC2=AD(AD+DB)∵AC=6,BD=5,
∴AD2+5AD-36=0,解得:AD=4,AD=-9(舍去),
∴AD=4.
故答案为:4.
点评:此题考查了相似三角形的判断与性质,是一道中档题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
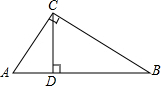 如图,Rt△ABC中,斜边为AB,且CD⊥AB于D,若AC:BC=1:
如图,Rt△ABC中,斜边为AB,且CD⊥AB于D,若AC:BC=1:| 3 |
| A、1:3 | ||
B、1:
| ||
| C、1:4 | ||
| D、2:3 |
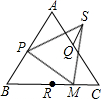 已知:如图,正三角形ABC中,P为AB的中点,Q为AC的中点,R为BC 的中点,M为RC上任意一点,△PMS为正三角形.求证:RM=QS.
已知:如图,正三角形ABC中,P为AB的中点,Q为AC的中点,R为BC 的中点,M为RC上任意一点,△PMS为正三角形.求证:RM=QS. (2012•西城区二模)如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若
(2012•西城区二模)如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若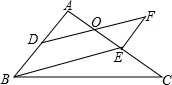 如图,△ABC中,D为AB的中点,E为AC上一点,过D作DF∥BE交AC于O,EF∥AB.
如图,△ABC中,D为AB的中点,E为AC上一点,过D作DF∥BE交AC于O,EF∥AB.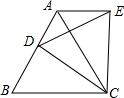 如图,在等边△ABC中,D为AB边上的动点(不与A、B重合),以CD为一边,向上作等边△EDC,连接AE.
如图,在等边△ABC中,D为AB边上的动点(不与A、B重合),以CD为一边,向上作等边△EDC,连接AE.