题目内容
如图：已知∠ACD=∠B，AD=4，BD=5，求AC的长．分析：直接根据相似三角形的判定定理即可得出△ABC∽△ACD，根据相似三角形的对应边成比例即可求出AC的长．
解答：解：∵∠ACD=∠B，∠A=∠A，
∴△ABC∽△ACD，
∴
=
，
∵AD=4，BD=5，
∴AB=9，
∴
=
，
∴AC=6，
答：AC的长是6．
∴△ABC∽△ACD，
∴
| AC |
| AB |
| AD |
| AC |
∵AD=4，BD=5，
∴AB=9，
∴
| AC |
| 9 |
| 4 |
| AC |
∴AC=6，
答：AC的长是6．
点评：本题考查的是相似三角形的判定与性质，用到的知识点为：①如果两三角形的两个角对应相等，那么这两个三角形相似；②相似三角形的对应边成比例．
练习册系列答案
相关题目
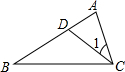如图，已知△ACD∽△ABC，∠1=∠B，下列各式正确的是（ ）A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图，已知△ACD∽△ADB，AC=4，AD=2，则AB的长为
如图，已知∠ACD=70°，∠ACB=60°，∠ABC=50°．
如图：已知∠ACD=∠B，