题目内容
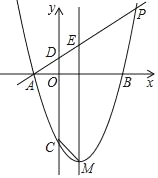
如图，在平面直角坐标系xOy中，抛物线y=x2+bx+c的对称轴为直线x=1，抛物线与x轴交于A、B两点（点A在点B的左侧），且AB=4，又P是抛物线上位于第一象限的点，直线AP与y轴交于点D，与对称轴交于点E，设点P的横坐标为t．
（1）求点A的坐标和抛物线的表达式；
（2）当AE：EP=1：2时，求点E的坐标；
（3）记抛物线的顶点为M，与y轴的交点为C，当四边形CDEM是等腰梯形时，求t的值．
练习册系列答案
名校课堂系列答案
相关题目
题目内容
如图，在平面直角坐标系xOy中，抛物线y=x2+bx+c的对称轴为直线x=1，抛物线与x轴交于A、B两点（点A在点B的左侧），且AB=4，又P是抛物线上位于第一象限的点，直线AP与y轴交于点D，与对称轴交于点E，设点P的横坐标为t．
（1）求点A的坐标和抛物线的表达式；
（2）当AE：EP=1：2时，求点E的坐标；
（3）记抛物线的顶点为M，与y轴的交点为C，当四边形CDEM是等腰梯形时，求t的值．
名校课堂系列答案
C. 
D. 2
