题目内容
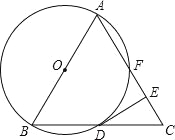
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
【答案】(1)证明见解析;(2)FE=1.
【解析】
试题分析:(1)连接OD,根据等边三角形的性质求出∠ODE=90°,根据切线的判定定理证明即可;
(2)连接AD,BF,根据等边三角形的性质求出DC、CF,根据直角三角形的性质求出EC,结合图形计算即可.
试题解析:(1)如图1,连接OD,∵△ABC是等边三角形,∴∠B=∠C=60°.
∵OB=OD,∴∠ODB=∠B=60°.∵DE⊥AC,∴∠DEC=90°.
∴∠EDC=30°.∴∠ODE=90°.∴DE⊥OD于点D.∵点D在⊙O上,
∴DE是⊙O的切线;
(2)如图2,连接AD,BF,∵AB为⊙O直径,∴∠AFB=∠ADB=90°.∴AF⊥BF,AD⊥BD.
∵△ABC是等边三角形,∴![]() ,
,![]() .
.
∵∠EDC=30°,∴![]() .∴FE=FC﹣EC=1.
.∴FE=FC﹣EC=1.



练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目



