题目内容
【题目】根据题意结合图形填空:已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.
答:是,理由如下:
∵AD⊥BC,EG⊥BC(已知)
∴∠4=∠5=90°( )
∴AD∥EG( )
∴∠1=∠E( )
∠2=∠3( )
∵∠E=∠3(已知)
∴(∠1)=(∠2)(等量代换)
∴AD是∠BAC的平分线( )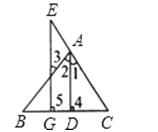
【答案】垂直定义;同位角相等,两条直线平行;两条直线平行,同位角相等;两条直线平行,内错角相等;角平分线定义
【解析】答:是,理由如下:
∵AD⊥BC,EG⊥BC(已知),
∴∠4=∠5=90°(垂直定义),
∴AD∥EG(同位角相等,两条直线平行),
∴∠1=∠E(两条直线平行,同位角相等),
∠2=∠3(两条直线平行,内错角相等);
∵∠E=∠3(已知),
∴∠1=∠2(等量代换),
∴AD是∠BAC的平分线(角平分线定义).
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质).

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目