题目内容
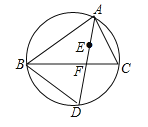
【题目】已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论正确个数的有( )
①DF⊥AB;②CG=2GA;③CG=DF+GE;④S四边形BFGC=![]() ﹣1.
﹣1.

A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】∵四边形ABCD是菱形,∴∠BAC=∠DAC,AB∥CD,∴∠1=∠ACD,
∵∠1=∠2,∴∠ACD=∠2,∴AE=ED,
∵GE⊥AD,∴AD=2AE,
∵AB=2AF,∴AE=AF,
又∵AG=AG,∴△FAG≌△EAF,∴∠AFG=∠AEG=90°,∴DF⊥AB,故①正确;
∵AB//CD,∴△AFG∽△CDG,∴CG:AG=CD:AF,∵AF=![]() AB,AB=CD,∴CG:AG=2:1,∴CG=2AG,故②正确;
AB,AB=CD,∴CG:AG=2:1,∴CG=2AG,故②正确;
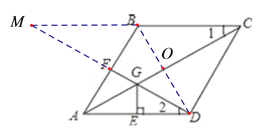
延长CB交DF的延长线于点,
∵AD//BC,∴∠M=∠2,∵∠1=∠2,∴∠1=∠M,∴CG=MG,
在△ADF和△BMF中,
∵∠M=∠2,∠BFM=∠AFD(对顶角相等),BF=AF,
∴△ADF≌△BMF(AAS),∴MF=DF,
∵△FAG≌△EAF,∴FG=EG,
∵GM=GF+MF,∴CG=DF+GE,故③正确;
由以上可得BO=1,AC=2![]() ,FG=
,FG=![]() ,
,
∴S四边形BFGC=S△ABC-S△AFG=![]() ×2
×2![]() ×1-
×1-![]() ×
×![]() ×1=
×1=![]() ,故④错误;
,故④错误;
故选C.

练习册系列答案
相关题目