题目内容
(2013年四川资阳9分)如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.

(1)若点D的坐标为(4,1),点E的坐标为(1,4):
①分别求出直线l与双曲线的解析式;
②若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.
解:(1)①把D(4,1)代入 得a=1×4=4,
得a=1×4=4,
∴反比例函数解析式为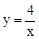 (x>0)。
(x>0)。
设直线l的解析式为y=kx+t,
把D(4,1),E(1,4)代入得 ,解得
,解得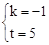 。
。
∴直线l的解析式为y=﹣x+5。
②直线l向下平移m(m>0)个单位得到y=﹣x+5﹣m,
当方程组 只有一组解时,直线l与双曲线有且只有一个交点,
只有一组解时,直线l与双曲线有且只有一个交点,
化为关于x的方程得x2+(5﹣m)x+4=0,
△=(m﹣5)2﹣4×4=0,解得m1=1,m2=9。
而m=9时,解得x=﹣2,故舍去。
∴当m=1时,直线l与双曲线有且只有一个交点。
(2)如图,作DF⊥x轴于点F,
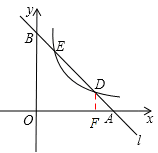
∵点D为线段AB的n等分点,∴DA:AB=1:n。
∵DF∥OB,∴△ADF∽△ABO。
∴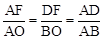 ,即
,即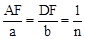 。
。
∴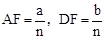 。∴OF=
。∴OF=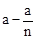 。
。
∴D点坐标为(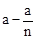 ,
, )。
)。
把D(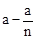 ,
, )代入
)代入 得(
得(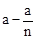 )•
)• =a,解得
=a,解得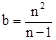 。
。
【解析】(1)①运用待定系数法可分别得到直线l与双曲线的解析式。
②直线l向下平移m(m>0)个单位得到y=﹣x+5﹣m,根据题意得方程组 只有一组解时,化为关于x的方程得x2+(5﹣m)x+4=0,则△=(m﹣5)2﹣4×4=0,解得m1=1,m2=9。当m=9时,公共点不在第一象限,所以m=1。
只有一组解时,化为关于x的方程得x2+(5﹣m)x+4=0,则△=(m﹣5)2﹣4×4=0,解得m1=1,m2=9。当m=9时,公共点不在第一象限,所以m=1。
(2)作DF⊥x轴,由DF∥OB得到△ADF∽△ABO,根据相似比可得到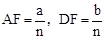 ,则D点坐标为(
,则D点坐标为(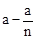 ,
, ),然后把D点坐标代入反比例函数解析式中即可得到b的值。
),然后把D点坐标代入反比例函数解析式中即可得到b的值。
考点:反比例函数综合题,待定系数法点的应用,曲线上点的坐标与方程的关系,一元二次方程根的判别式,相似三角形的判定和性质。

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
 cm/s速度沿AC向点C运动,运动时间为t(t>0);
cm/s速度沿AC向点C运动,运动时间为t(t>0); ≈1.4,
≈1.4, ≈1.7)
≈1.7)

 中.
中.