题目内容
已知如下一元二次方程:第1个方程:3x2+2x-1=0;
第2个方程:5x2+4x-1=0;
第3个方程:7x2+6x-1=0;
…
按照上述方程的二次项系数、一次项系数、常数项的排列规律,则第8个方程为 ;第n(n为正整数)个方程为 ,其两个实数根为 .
【答案】分析:观察一元二次方程二次项系数、一次项系数和常数项得到二次项系数为序号的两倍加1,一次项系数为序号的两倍,常数项不变为-1,即第n(n为正整数)个方程为(2n+1)x2+2nx-1=0,然后利用因式分解法解方程即可.
解答:解:∵二次项系数为序号的两倍加1,一次项系数为序号的两倍,常数项不变为-1,
∴第8个方程为17x2+16x-1=0;
第n(n为正整数)个方程为(2n+1)x2+2nx-1=0,
∵[(2n+1)x-1][x+1]=0,
∴(2n+1)x-1=0或x+1=0,
∴x1=-1,x2=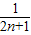 .
.
故答案为17x2+16x-1=0;(2n+1)x2+2nx-1=0;x1=-1,x2=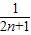 .
.
点评:本题考查了关于数字变化的规律:通过观察数字之间的变化规律,得到一般性的结论,再利用此结论解决问题.
解答:解:∵二次项系数为序号的两倍加1,一次项系数为序号的两倍,常数项不变为-1,
∴第8个方程为17x2+16x-1=0;
第n(n为正整数)个方程为(2n+1)x2+2nx-1=0,
∵[(2n+1)x-1][x+1]=0,
∴(2n+1)x-1=0或x+1=0,
∴x1=-1,x2=
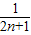 .
.故答案为17x2+16x-1=0;(2n+1)x2+2nx-1=0;x1=-1,x2=
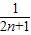 .
.点评:本题考查了关于数字变化的规律:通过观察数字之间的变化规律,得到一般性的结论,再利用此结论解决问题.

练习册系列答案
相关题目
 ;
; ;
; ;
¼¼
;
¼¼ (
(