题目内容
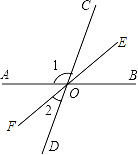
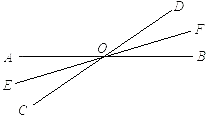
如下图,已知直线AB、CD相交于点O,OE、OF分别是∠AOC、∠BOD的平分线,设∠AOC=30°,求∠EOF。
解:∵∠AOC+∠BOC=∠BOC+∠BOD
∴∠BOD=∠( )=( )度,
∵∠BOC=∠( )=( )度,
∵OE、OF分别是∠AOC、∠BOD的平分线,
∴∠EOC=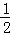 ∠AOC,∠BOF=( ),
∠AOC,∠BOF=( ),
∴∠EOC+∠BOF+∠BOC=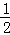 ( )+( )+∠BOC=∠AOC+∠BOC=180°,
( )+( )+∠BOC=∠AOC+∠BOC=180°,
即∠EOF=180度。
解:∵∠AOC+∠BOC=∠BOC+∠BOD
∴∠BOD=∠( )=( )度,
∵∠BOC=∠( )=( )度,
∵OE、OF分别是∠AOC、∠BOD的平分线,
∴∠EOC=
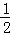 ∠AOC,∠BOF=( ),
∠AOC,∠BOF=( ),∴∠EOC+∠BOF+∠BOC=
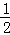 ( )+( )+∠BOC=∠AOC+∠BOC=180°,
( )+( )+∠BOC=∠AOC+∠BOC=180°,即∠EOF=180度。
解:∠AOC;30;∠AOD;150;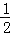 ∠BOD;∠AOC;∠BOD。
∠BOD;∠AOC;∠BOD。
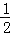 ∠BOD;∠AOC;∠BOD。
∠BOD;∠AOC;∠BOD。
练习册系列答案
相关题目
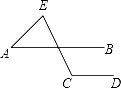
 27、尺规作图题(保留作图痕迹,不写作法,共5分)
27、尺规作图题(保留作图痕迹,不写作法,共5分) 尺规作图题(保留作图痕迹,不写作法)
尺规作图题(保留作图痕迹,不写作法)