题目内容
【题目】(本小题满分9分)点A,B,C在数轴上表示数a,b,c,满足(b+2)2+(c–24)2=0,多项式x|a+3|y2–ax3y+xy2–1是关于字母x,y的五次多项式.
(1)a的值__________,b的值__________,c的值__________.
(2)已知蚂蚁从A点出发,以每秒3 cm的速度爬行,先到点B,再到点C,一共需要多长时间?(精确到秒)
(3)求值:a2b–bc.
【答案】见解析
【解析】(1)∵(b+2)2≥0,(c–24)2≥0,且(b+2)2+(c–24)2=0,
∴b+2=0,c–24=0,即b=–2,c=24,
∵x|a+3|y2–ax3y+xy2–1是关于x、y的五次多项式,∴|a+3|=3,∴a=0或a=–6.
故:a=0或–6,b=–2,c=24.(3分)
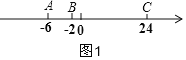
(2)当点A对应–6时,如图1,AC=24–(–6)=30(cm),30÷3=10(秒),
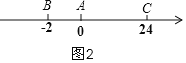
当点A对应0时,如图2,蚂蚁的路程为:AB+BC=2+26=28(cm),
28÷3=9![]() (秒)≈9(秒),
(秒)≈9(秒),
答:需要10秒或9秒时间到达点C.(6分)
(3)①当a=0,b=–2,c=24时,a2b–bc=0–(–2)×24=48,
②当a=–6,b=–2,c=24时,a2b–bc=(–6)2×(–2)–(–2)×24=–72+48=–24.(9分)

练习册系列答案
相关题目


