题目内容
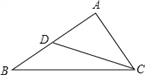
【题目】如图，已知在△ABC中，D是AB的中点，且∠ACD=∠B，若 AB=10，求AC的长．
【答案】5
.
【解析】试题分析：
由点D是AB的中点，AB=10，易得AD=5；再由∠ACD=∠B，∠A=∠A，可证得：
△ACD∽△ABC，从而可得： 
，由此得到：AC2=AD
AB=50即可解得AC的值.
试题解析：
∵∠ACD=∠B，∠A=∠A，
∴△ACD∽△ABC．
∴
，
∴AC2=AD
AB.
∵D是AB的中点，AB=10，
∴AD=
AB=5,
∴AC2=50．
解得AC=
.
【题型】解答题
【结束】
22
【题目】口袋中装有四个大小完全相同的小球，把它们分别标号1,2,3,4，从中随机摸出一个球，记下数字后放回，再从中随机摸出一个球，利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】
.
【解析】试题分析：
根据题意列表如下，由表可以得到所有的等可能结果，再求出所有结果中，两次所摸到小球的数字之和为4的次数，即可计算得到所求概率.
试题解析：
列表如下：
1 | 2 | 3 | 4 | |
1 | （1，1） | （1，2） | （1，3） | （1，4） |
2 | （2，1） | （2，2） | （2，3） | （2，4） |
3 | （3，1） | （3，2） | （3，3） | （3，4） |
4 | （4，1） | （4，2） | （4，3） | （4，4） |
由表可知，共有16种等可能事件，其中两次摸到的小球数字之和等于4的有（3，1）、（2，2）和（1，3），共计3种，
∴P（两次摸到小球的数字之和等于4）=
.
【题目】进入六月以来，西瓜出现热卖．佳佳水果超市用760元购进甲、乙两个品种的西瓜，销售完共获利360元，其进价和售价如表：
甲品种 | 乙品种 | |
进价（元/千克） | 1.6 | 1.4 |
售价（元/千克） | 2.4 | 2 |
（1）求佳佳水果超市购进甲、乙两个品种的西瓜各多少千克？
（2）由于销售较好，该超市决定，按进价再购进甲，乙两个品种西瓜，购进乙品种西瓜的重量不变，购进甲品种西瓜的重量是原来的2倍，甲品种西瓜按原价销售，乙品种西瓜让利销售．若两个品种的西瓜售完获利不少于560元，问乙品种西瓜最低售价为多少元？
【题目】为了更好治理某湖水质，保护环境，市治污公司决定购买
台污水处理设备．现有
，
两种型号的设备，其中每台的价格，月处理污水量如下表．经调查：购买一台型设备比购买一台型设备多
万元，购买台型设备比购买
台型设备少
万元．
|
| |
价格（万元/台） |
|
|
处理污水量（吨/月） |
|
|
（
）求
，
的值．
（）经预算：市治污公司购买污水处理设备的资金不超过
万元，你认为该公司有哪几种购买方案．
（）在（）问的条件下，若每月要求处理该湖的污水量不低于
吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．
