题目内容
如图,已知直线 ,
, 被直线
被直线 所截,在括号内为下面各小题的推理填上适当的根据.
所截,在括号内为下面各小题的推理填上适当的根据.

(1)∵ ∥
∥ ,∴∠1=∠3( );
,∴∠1=∠3( );
(2)∵∠1=∠3,∴ ∥
∥ ( );
( );
(3)∵ ∥
∥ ,∴∠1=∠2( );
,∴∠1=∠2( );
(4)∵ ∥
∥ ,∴∠1+∠4=180°( );
,∴∠1+∠4=180°( );
(5)∵∠1=∠2,∴ ∥
∥ ( );
( );
(6)∵∠1+∠4=180°,∴ ∥
∥ ( ).
( ).
 ,
, 被直线
被直线 所截,在括号内为下面各小题的推理填上适当的根据.
所截,在括号内为下面各小题的推理填上适当的根据.
(1)∵
 ∥
∥ ,∴∠1=∠3( );
,∴∠1=∠3( ); (2)∵∠1=∠3,∴
 ∥
∥ ( );
( );(3)∵
 ∥
∥ ,∴∠1=∠2( );
,∴∠1=∠2( );(4)∵
 ∥
∥ ,∴∠1+∠4=180°( );
,∴∠1+∠4=180°( );(5)∵∠1=∠2,∴
 ∥
∥ ( );
( );(6)∵∠1+∠4=180°,∴
 ∥
∥ ( ).
( ). (1)两直线平行,同位角相等;(2)同位角相等,两直线平行;(3)两直线平行,内错角相等;(4)两直线平行,同旁内角互补;(5)内错角相等,两直线平行;(6)同旁内角互补,两直线平行
试题分析:根据平行线的判定和性质依次分析即可作出判断.
(1)∵
 ∥
∥ ,∴∠1=∠3(两直线平行,同位角相等);
,∴∠1=∠3(两直线平行,同位角相等); (2)∵∠1=∠3,∴
 ∥
∥ (同位角相等,两直线平行);
(同位角相等,两直线平行);(3)∵
 ∥
∥ ,∴∠1=∠2(两直线平行,内错角相等);
,∴∠1=∠2(两直线平行,内错角相等);(4)∵
 ∥
∥ ,∴∠1+∠4=180°(两直线平行,同旁内角互补);
,∴∠1+∠4=180°(两直线平行,同旁内角互补);(5)∵∠1=∠2,∴
 ∥
∥ (内错角相等,两直线平行);
(内错角相等,两直线平行);(6)∵∠1+∠4=180°,∴
 ∥
∥ (同旁内角互补,两直线平行).
(同旁内角互补,两直线平行). 点评:本题属于基础应用题,只需学生熟练掌握平行线的判定和性质,即可完成.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目


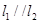 则∠
则∠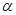
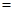 ( )
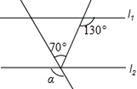
( )
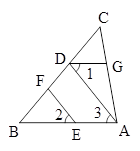

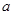 ∥
∥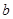 ,∠4=40°,则∠2= .
,∠4=40°,则∠2= .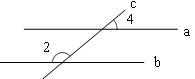
 ,∠CFP=∠
,∠CFP=∠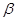 ,∠EPF=∠
,∠EPF=∠ 。
。