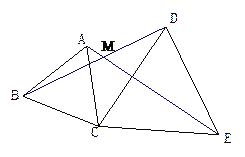
题目内容
【题目】如图,把△ACE绕点C逆时针旋转60°后与△BCD重合,BD、AE.交于点 M,连接AB、DE.
(1)求证:△ABC和△CDE为等边三角形;
(2)求∠AMB的度数.
【答案】(1)证明见解析;(2)60°.
【解析】试题分析:(1)由旋转的性质易得△ABC和△DCE是等边三角形;
(2)由旋转可知△BCD≌ACE,从而∠CAE=∠CBD,故可得∠AMB=180°-∠BAM-∠ABM=180°-∠BAC-∠CAE-∠ABM=60°.
试题解析:(1)证明:由旋转可知:
BC=CA,CD=CE,∠BAC=∠DCE=60°,
∴△ABC和△DCE是等边三角形.
(2)由旋转可知△BCD≌ACE,
∴∠CAE=∠CBD,
∠AMB=180°-∠BAM-∠ABM=180°-∠BAC-∠CAE-∠ABM
=180°-∠BAC-(∠CAE+∠ABM)
=180°-∠BAC-(∠CDB+∠ABM)
=180°-∠BAC-ABC=180°-60°-60°=60°.

【题目】(本小题满分10分)小红的妈妈开了间海产品干货店,今年从沿海地区进了一批墨鱼干,以60元/千克的价格销售,由于墨鱼干质量好,价格便宜,加上来旅游的顾客很多,一时间销售了不少.妈妈看到生意红火,决定经过提价来增加利润.于是先后将售价提高到80元/千克和100元/千克,销售量依次减少了,但每天的利润依次增加,然后她又把售价调到140元/千克,此时过往的顾客大多数嫌贵,销售量明显下降,连利润也呈下降趋势.面对如此情况,小红思考了一个问题:售价究竟定为多少才使每天的利润最大呢?
小红看了妈妈的账单后马上进行了分析调查,从账单上了解到如下数据:
售价(元/千克) | 60 | 80 | 100 | 120 | 140 |
每天销售量(千克) | 22.5 | 20 | 17.5 | 15 | 12.5 |
请你利用数学知识帮小红计算一下,
(1)设销售量为y千克,售价为x元,y与x之间的关系式.
(2)售价究竟定为多少元才能每天的销售额最大. (销售额=售价![]() 销售量)
销售量)







