题目内容
在课外兴趣小组活动时,刘老师给出了如下问题:
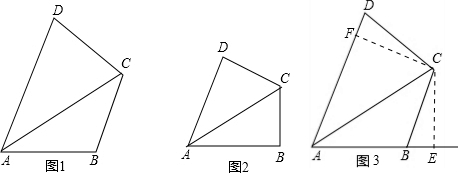
如图(1),已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,求证:AB+AD=
AC.
小敏反复探索,不得其解.她想,若将四边形ABCD特殊化,看如何解决该问题.
(1)从特殊情况入手,添加条件“∠B=∠D”,如图(2),可证:AB+AD=
AC.请你完成此证明.
(2)类比(1)的问题的解决方法,在图(1)证明AB+AD=
AC.
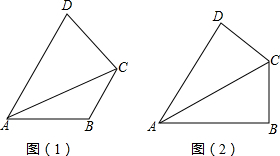
如图(1),已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,求证:AB+AD=
| 3 |
小敏反复探索,不得其解.她想,若将四边形ABCD特殊化,看如何解决该问题.
(1)从特殊情况入手,添加条件“∠B=∠D”,如图(2),可证:AB+AD=
| 3 |
(2)类比(1)的问题的解决方法,在图(1)证明AB+AD=
| 3 |

分析:(1)如果:“∠B=∠D”,根据∠B与∠D互补,那么∠B=∠D=90°,又因为∠DAC=∠BAC=30°,因此我们可在直角三角形ADC和ABC中得出AD=AB=
AC,那么AD+AB=
AC.
(2)按(1)的思路,作好辅助线后,我们只要证明△CDF与△CBE全等即可得到(1)的条件.根据AAS可证两三角形全等,DF=BE.然后按照(1)的解法进行计算即可.
| ||
| 2 |
| 3 |
(2)按(1)的思路,作好辅助线后,我们只要证明△CDF与△CBE全等即可得到(1)的条件.根据AAS可证两三角形全等,DF=BE.然后按照(1)的解法进行计算即可.
解答:(1)证明:在题图(2)中,
∵∠B=∠D,且∠B与∠D互补,
∴∠B=∠D=90°.
又∵AC平分∠DAB,∠DAB=60°,
∴∠CAB=∠CAD=30°,
∴AB=AC×cos∠CAB=
AC,
AD=AC×cos∠CAD=
AC,
∴AB+AD=
AC.
(2)证明:如图,过C点分别作AB、AD的垂线,垂足分别为E、F.
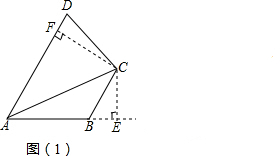
由(1)知,AE+AF=
AC.
∵AC为∠BAD的平分线,CF⊥AD,CE⊥AB,
∴∠CFD=∠CEB,CE=CF.
而∠ABC与∠D互补,∠ABC与∠CBE也互补,
∴∠D=∠CBE,
在△CDF与△CBE中,
∴△CDF与△CBE(AAS),
∴DF=BE,
∴AB+AD=AB+(AF+FD)=(AB+BE)+AF=AE+AF=
AC.
∵∠B=∠D,且∠B与∠D互补,
∴∠B=∠D=90°.
又∵AC平分∠DAB,∠DAB=60°,
∴∠CAB=∠CAD=30°,
∴AB=AC×cos∠CAB=
| ||
| 2 |
AD=AC×cos∠CAD=
| ||
| 2 |
∴AB+AD=
| 3 |
(2)证明:如图,过C点分别作AB、AD的垂线,垂足分别为E、F.

由(1)知,AE+AF=
| 3 |
∵AC为∠BAD的平分线,CF⊥AD,CE⊥AB,
∴∠CFD=∠CEB,CE=CF.
而∠ABC与∠D互补,∠ABC与∠CBE也互补,
∴∠D=∠CBE,
在△CDF与△CBE中,
|
∴△CDF与△CBE(AAS),
∴DF=BE,
∴AB+AD=AB+(AF+FD)=(AB+BE)+AF=AE+AF=
| 3 |
点评:本题考查了由特殊到一般的探究能力.通过对特殊问题解法的类比、发散联想,进行创造性思维,从而延伸到一般问题的解题方法.解本题的关键是将(1)中的做法应用到(2)中时恰当添加辅助线.

练习册系列答案
相关题目