题目内容
【题目】如图,直线l:y=﹣ ![]() x,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3 , …,按此做法进行下去,点A2016的坐标为 .
x,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3 , …,按此做法进行下去,点A2016的坐标为 . 
【答案】![]()
【解析】解:∵点A1坐标为(﹣3,0),
∴OA1=3,
∵在y=﹣ ![]() x中,当x=﹣3时,y=4,即B1点的坐标为(﹣3,4),
x中,当x=﹣3时,y=4,即B1点的坐标为(﹣3,4),
∴由勾股定理可得OB1= ![]() =5,即OA2=5=3×
=5,即OA2=5=3× ![]() ,
,
同理可得,
OB2= ![]() ,即OA3=
,即OA3= ![]() =3×(
=3×( ![]() )2 ,
)2 ,
OB3= ![]() ,即OA4=
,即OA4= ![]() =3×(
=3×( ![]() )3 ,
)3 ,
以此类推,
OAn=3×( ![]() )n﹣1=
)n﹣1= ![]() ,即点An坐标为(﹣
,即点An坐标为(﹣ ![]() ,0),
,0),
当n=2016时,点A2016坐标为(﹣ ![]() ,0).
,0).
所以答案是:(﹣ ![]() ,0)
,0)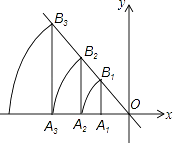
【考点精析】认真审题,首先需要了解一次函数的性质(一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小).

练习册系列答案
相关题目







