题目内容
我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2-2x-3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C.(1)求经过点C的“蛋圆”的切线的表达式;
(2)求经过点D的“蛋圆”的切线的表达式;
(3)已知点E是“蛋圆”上一点(不与点A、点B重合),点E关于x轴的对称点是F,若点F也在“蛋圆”上,求点E的坐标.

【答案】分析:(1)根据题意,先求得C点坐标,然后根据三角形性质求出G点坐标,用待定系数法求出直线EC的解析式;
(2)因为经过点D的“蛋圆”切线过D点,所以本题可设它的解析式为y=kx-3.根据图象可求出抛物线的解析式,因为相切,所以它们的交点只有一个,进而可根据一元二次方程的有关知识解决问题;
(3)假设点E在x轴上方的“蛋圆”上,EF与x轴交于点H,连接EM.由HM2+EH2=EM2,点F在二次函数y=x2-2x-3的图象上,可得方程组,以及对称性求解.
解答: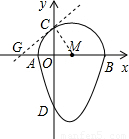 解:(1)由题意得:A(-1,0),B(3,0),D(0,-3),M(1,0).
解:(1)由题意得:A(-1,0),B(3,0),D(0,-3),M(1,0).
∴AM=BM=CM=2,
∴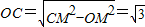 ,
,
∴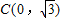
∵GC是⊙M的切线,
∴∠GCM=90°
∴cos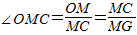 ,
,
∴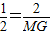 ,
,
∴MG=4,
∴G(-3,0),
∴直线GC的表达式为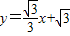 ;
;
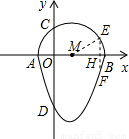 (2)设过点D的直线表达式为y=kx-3,
(2)设过点D的直线表达式为y=kx-3,
∴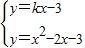
∴x2-(2+k)x=0,或x1=0,x2=2+k△=[-(2+k)]2=0,或x1=x2,
∴k=-2,
∴过点D的“蛋圆”的切线的表达式为y=-2x-3.
(3)假设点E在x轴上方的“蛋圆”上,设E(m,n),则点F的坐标为(m,-n).
EF与x轴交于点H,连接EM.
∴HM2+EH2=EM2,
∴(m-1)2+n2=4,…①;
∵点F在二次函数y=x2-2x-3的图象上,
∴m2-2m-3=-n,…②
解由①②组成的方程组得: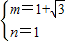 ;
;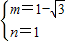 .(n=0舍去)
.(n=0舍去)
由对称性可得: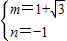 ;
;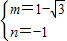 .
.
∴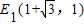 ,
, ,
,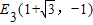 ,
,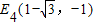 .
.
点评:考查了二次函数综合题,此类题目需灵活运用待定系数法建立函数解析式,并利用切线的性质,结合方程思想来解决问题.
(2)因为经过点D的“蛋圆”切线过D点,所以本题可设它的解析式为y=kx-3.根据图象可求出抛物线的解析式,因为相切,所以它们的交点只有一个,进而可根据一元二次方程的有关知识解决问题;
(3)假设点E在x轴上方的“蛋圆”上,EF与x轴交于点H,连接EM.由HM2+EH2=EM2,点F在二次函数y=x2-2x-3的图象上,可得方程组,以及对称性求解.
解答:
 解:(1)由题意得:A(-1,0),B(3,0),D(0,-3),M(1,0).
解:(1)由题意得:A(-1,0),B(3,0),D(0,-3),M(1,0).∴AM=BM=CM=2,
∴
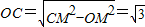 ,
,∴
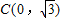
∵GC是⊙M的切线,
∴∠GCM=90°
∴cos
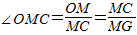 ,
,∴
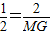 ,
,∴MG=4,
∴G(-3,0),
∴直线GC的表达式为
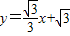 ;
;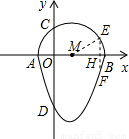 (2)设过点D的直线表达式为y=kx-3,
(2)设过点D的直线表达式为y=kx-3,∴
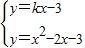
∴x2-(2+k)x=0,或x1=0,x2=2+k△=[-(2+k)]2=0,或x1=x2,
∴k=-2,
∴过点D的“蛋圆”的切线的表达式为y=-2x-3.
(3)假设点E在x轴上方的“蛋圆”上,设E(m,n),则点F的坐标为(m,-n).
EF与x轴交于点H,连接EM.
∴HM2+EH2=EM2,
∴(m-1)2+n2=4,…①;
∵点F在二次函数y=x2-2x-3的图象上,
∴m2-2m-3=-n,…②
解由①②组成的方程组得:
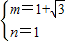 ;
;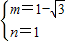 .(n=0舍去)
.(n=0舍去)由对称性可得:
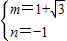 ;
;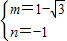 .
.∴
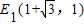 ,
, ,
,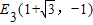 ,
,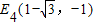 .
.点评:考查了二次函数综合题,此类题目需灵活运用待定系数法建立函数解析式,并利用切线的性质,结合方程思想来解决问题.

练习册系列答案
相关题目
 (2013•通州区一模)我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2-2x-3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C.
(2013•通州区一模)我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2-2x-3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C. 我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2-2x-3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C.
我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2-2x-3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C.