��Ŀ����
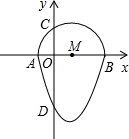 ��2013•ͨ����һģ�����ǰ�һ����Բ����κ���ͼ���һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣨��Բ����κ���ͼ������ӵ���⣩����ô����ֱ�߽�������Բ�������ߣ���ͼ�����κ���y=x2-2x-3��ͼ����x�ύ�ڵ�A��B����y�ύ�ڵ�D��ABΪ��Բֱ������ԲԲ��Ϊ��M����Բ��y��������ύ�ڵ�C��
��2013•ͨ����һģ�����ǰ�һ����Բ����κ���ͼ���һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣨��Բ����κ���ͼ������ӵ���⣩����ô����ֱ�߽�������Բ�������ߣ���ͼ�����κ���y=x2-2x-3��ͼ����x�ύ�ڵ�A��B����y�ύ�ڵ�D��ABΪ��Բֱ������ԲԲ��Ϊ��M����Բ��y��������ύ�ڵ�C����1������C�ġ���Բ�������ߵı���ʽ��
��2������D�ġ���Բ�������ߵı���ʽ��
��3����֪��E�ǡ���Բ����һ�㣨�����A����B�غϣ�����E����x��ĶԳƵ���F������FҲ�ڡ���Բ���ϣ����E�����꣮
��������1���������⣬�����C�����꣬Ȼ������������������G�����꣬�ô���ϵ�������ֱ��EC�Ľ���ʽ��
��2����Ϊ������D�ġ���Բ�����߹�D�㣬���Ա���������Ľ���ʽΪy=kx-3������ͼ�����������ߵĽ���ʽ����Ϊ���У��������ǵĽ���ֻ��һ���������ɸ���һԪ���η��̵��й�֪ʶ������⣻
��3�������E��x���Ϸ��ġ���Բ���ϣ�EF��x�ύ�ڵ�H������EM����HM2+EH2=EM2����F�ڶ��κ���y=x2-2x-3��ͼ���ϣ��ɵ÷����飬�Լ��Գ�����⣮
��2����Ϊ������D�ġ���Բ�����߹�D�㣬���Ա���������Ľ���ʽΪy=kx-3������ͼ�����������ߵĽ���ʽ����Ϊ���У��������ǵĽ���ֻ��һ���������ɸ���һԪ���η��̵��й�֪ʶ������⣻
��3�������E��x���Ϸ��ġ���Բ���ϣ�EF��x�ύ�ڵ�H������EM����HM2+EH2=EM2����F�ڶ��κ���y=x2-2x-3��ͼ���ϣ��ɵ÷����飬�Լ��Գ�����⣮
���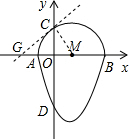 �⣺��1��������ã�A��-1��0����B��3��0����D��0��-3����M��1��0����
�⣺��1��������ã�A��-1��0����B��3��0����D��0��-3����M��1��0����
��AM=BM=CM=2��
��OC=
=
��
��C(0��
)
��GC�ǡ�M�����ߣ�
���GCM=90��
��cos��OMC=
=
��
��
=
��
��MG=4��
��G��-3��0����
��ֱ��GC�ı���ʽΪy=
x+
��
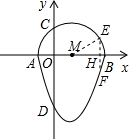 ��2�������D��ֱ�߱���ʽΪy=kx-3��
��2�������D��ֱ�߱���ʽΪy=kx-3��
��
��x2-��2+k��x=0����x1=0��x2=2+k��=[-��2+k��]2=0����x1=x2��
��k=-2��
�����D�ġ���Բ�������ߵı���ʽΪy=-2x-3��
��3�������E��x���Ϸ��ġ���Բ���ϣ���E��m��n�������F������Ϊ��m��-n����
EF��x�ύ�ڵ�H������EM��
��HM2+EH2=EM2��
�ࣨm-1��2+n2=4�����٣�
�ߵ�F�ڶ��κ���y=x2-2x-3��ͼ���ϣ�
��m2-2m-3=-n������
���ɢ٢���ɵķ�����ã�
��
����n=0��ȥ��
�ɶԳ��Կɵã�
��
��
��E1(1+
��1)��E2(1-
��1)��E3(1+
��-1)��E4(1-
��-1)��
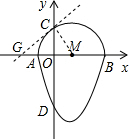 �⣺��1��������ã�A��-1��0����B��3��0����D��0��-3����M��1��0����
�⣺��1��������ã�A��-1��0����B��3��0����D��0��-3����M��1��0������AM=BM=CM=2��
��OC=
| CM2-OM2 |
| 3 |
��C(0��
| 3 |
��GC�ǡ�M�����ߣ�
���GCM=90��
��cos��OMC=
| OM |
| MC |
| MC |
| MG |
��
| 1 |
| 2 |
| 2 |
| MG |
��MG=4��
��G��-3��0����
��ֱ��GC�ı���ʽΪy=
| ||
| 3 |
| 3 |
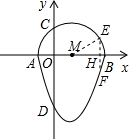 ��2�������D��ֱ�߱���ʽΪy=kx-3��
��2�������D��ֱ�߱���ʽΪy=kx-3����
|
��x2-��2+k��x=0����x1=0��x2=2+k��=[-��2+k��]2=0����x1=x2��
��k=-2��
�����D�ġ���Բ�������ߵı���ʽΪy=-2x-3��
��3�������E��x���Ϸ��ġ���Բ���ϣ���E��m��n�������F������Ϊ��m��-n����
EF��x�ύ�ڵ�H������EM��
��HM2+EH2=EM2��
�ࣨm-1��2+n2=4�����٣�
�ߵ�F�ڶ��κ���y=x2-2x-3��ͼ���ϣ�
��m2-2m-3=-n������
���ɢ٢���ɵķ�����ã�
|
|
�ɶԳ��Կɵã�
|
|
��E1(1+
| 3 |
| 3 |
| 3 |
| 3 |
�����������˶��κ����ۺ��⣬������Ŀ��������ô���ϵ����������������ʽ�����������ߵ����ʣ���Ϸ���˼����������⣮

��ϰ��ϵ�д�
 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
�����Ŀ
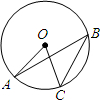 ��2013•ͨ����һģ����ͼ��A��B��C�ǡ�O�ϵ������㣬��ABC=32�㣬���AOC�Ķ����ǣ�������
��2013•ͨ����һģ����ͼ��A��B��C�ǡ�O�ϵ������㣬��ABC=32�㣬���AOC�Ķ����ǣ�������
 ��2013•ͨ����һģ����ͼ��AB��CD����E��AB�ϣ���DC=DE����AEC=70�㣬���D�Ķ�����
��2013•ͨ����һģ����ͼ��AB��CD����E��AB�ϣ���DC=DE����AEC=70�㣬���D�Ķ�����