题目内容
（2004•河南）如图，AB为半圆O的直径，在AB的同侧作AC、BD切半圆O于A、B，CD切半圆O于E．请分别写出两个角相等、两条边相等、两个三角形全等、两个三角形相似等四个正确的结论．
【答案】分析：根据题意写出符合规定的结论即可．
解答：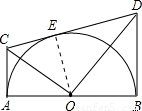
解：连接OE，由切线长定理知，AC=CE，ED=BD，∠ACO=∠OCE，∠EDO=∠BDO，
由SAS可证得△ACO≌△ECO，△EDO≌△BDO，
有∠AOC=∠COE，∠BOD=∠EOD，故有∠COD=90°，
又有OE⊥CD，
∴△CEO∽△OED，∴△ACO∽△OED．
点评：本题答案不唯一，利用了切线长定理，切线的性质，全等三角形相似三角形的判定求解．
解答：
解：连接OE，由切线长定理知，AC=CE，ED=BD，∠ACO=∠OCE，∠EDO=∠BDO，由SAS可证得△ACO≌△ECO，△EDO≌△BDO，
有∠AOC=∠COE，∠BOD=∠EOD，故有∠COD=90°，
又有OE⊥CD，
∴△CEO∽△OED，∴△ACO∽△OED．
点评：本题答案不唯一，利用了切线长定理，切线的性质，全等三角形相似三角形的判定求解．
练习册系列答案
相关题目
