题目内容
(1)善于思考的小迪发现:半径为a,圆心在原点的圆(如图1),如果固定直径AB,把圆内的所有与y轴平行的弦都压缩到原来的 倍,就得到一种新的图形-椭圆(如图2).她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”、“化曲为直,以直代曲”的方法,正确地求出了椭圆的面积,她求得的结果为 ;
倍,就得到一种新的图形-椭圆(如图2).她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”、“化曲为直,以直代曲”的方法,正确地求出了椭圆的面积,她求得的结果为 ;(2)小迪把图2的椭圆绕x轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为a的球的体积为
 πa3,则此椭球的体积为 .
πa3,则此椭球的体积为 .
【答案】分析:本题需先认真审题再解得:
(1)依据“化整为零,积零为整”、“化曲为直,以直代曲”的方法,结合圆的面积求法即可得;
(2)运用球的体积公式乘以(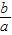 )2即可得.
)2即可得.
解答:解:(1)根据“化整为零,积零为整”、“化曲为直,以直代曲”的方法,结合圆的面积求法可知,椭圆的面积为π•a•a•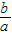 =πab;
=πab;
(2)因为半径为a的球的体积为 πa3,所以椭球的体积为:
πa3,所以椭球的体积为: πa3(
πa3(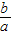 )2=
)2= πab2.
πab2.
点评:此题主要考查了学生的阅读分析能力和类比推理的思维能力.要熟练掌握圆的面积公式并会从题意中找到类比的规律,从而求解.
(1)依据“化整为零,积零为整”、“化曲为直,以直代曲”的方法,结合圆的面积求法即可得;
(2)运用球的体积公式乘以(
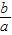 )2即可得.
)2即可得.解答:解:(1)根据“化整为零,积零为整”、“化曲为直,以直代曲”的方法,结合圆的面积求法可知,椭圆的面积为π•a•a•
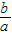 =πab;
=πab;(2)因为半径为a的球的体积为
 πa3,所以椭球的体积为:
πa3,所以椭球的体积为: πa3(
πa3(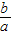 )2=
)2= πab2.
πab2.点评:此题主要考查了学生的阅读分析能力和类比推理的思维能力.要熟练掌握圆的面积公式并会从题意中找到类比的规律,从而求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
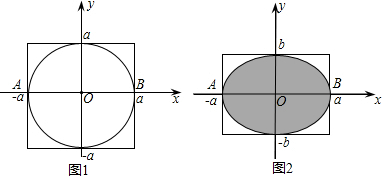 鸡蛋型”的椭球.已知半径为a的球的体积为
鸡蛋型”的椭球.已知半径为a的球的体积为 ,圆心在原点的圆(如图1),如果固定直径
,圆心在原点的圆(如图1),如果固定直径 ,把圆内的所有与
,把圆内的所有与 轴平行的弦都压缩到原来的
轴平行的弦都压缩到原来的 倍,就得到一种新的图形
倍,就得到一种新的图形 椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .
椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .
 轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为
轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为 ,则此椭球的体积为 .
,则此椭球的体积为 . 倍,就得到一种新的图形------椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .
倍,就得到一种新的图形------椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为 .