Question

某住宅小区将要举办“迎奥运”知识竞赛，物业的工作人员在购买奖品时，了解到如下信息：

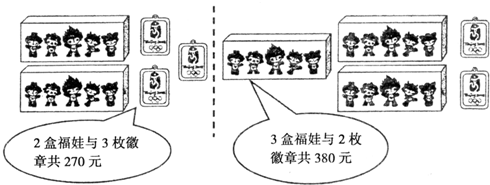
（1）求一盒“福娃”和一枚徽章各多少元？
（2）物业公司公布本次活动奖品发放方案如下：

一等奖	二等奖	三等奖
1盒福娃和1枚徽章	1盒福娃	1枚徽章

如果在这次活动中，用于购买奖品的总费用不少于1500元但不超过1600元，设一、二、三等奖共20名，其中一等奖2名，那么二等奖和三等奖应各设多少名？

Answer 1

分析：（1）首先根据题意设一盒“福娃”x元，一枚徽章y元，再根据等量关系为：2盒福娃价格+3枚徽章价格=270元，3盒福娃价格+2枚徽章价格=380元，可以列出方程组，解可得答案；
（2）二等奖a名，则三等奖（20-2-a）名，根据不等关系“总费用不少于1500元但不超过1600元”可得不等式组，解不等式组，求出整数解即可．

解答：解：（1）设一盒“福娃”x元，一枚徽章y元，由题意得：

2x+3y=270 3x+2y=380

，
解得：

x=120 y=10

，
答：一盒“福娃”120元，一枚徽章10元；

（2）设二等奖a名，则三等奖（20-2-a）名，由题意得：

120a+10(20-2-a)+2×120+2×10≥1500 120a+10(20-2-a)+2×120+2×10≤1600

，
解得：9

7

11

≤a≤10

6

11

，
∵a为整数，
∴a=10，
则三等奖人数为：20-2-10=8（名），
答：二等奖10名，则三等奖8名．

点评：此题主要考查了二元一次方程组的应用，不等式组的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组或不等式组，再求解．