题目内容

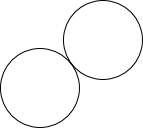
如图，⊙O1和⊙O2外切于点T，它们的半径之比为3：2，AB是它们的外公切线，A、B是切点，AB=4
6
，那么⊙O1和⊙O2的圆心距是（　　）
A．5
6
B．10
6
C．10D．
20
39
13

连接O1A，O2B．
设两圆的半径分别是2x，3x，
则O1O2=5x，O1C=x；
根据勾股定理，得
25x2=x2+96，
x=2．
则O1O2=5x=10．
故选C．
练习册系列答案
相关题目
如果⊙O1和⊙O2相交于C、E，CB是⊙O1的直径，过B作⊙O1的切线交CE的延长线于A，AFD是割线，交⊙O2于F、D，BC=FD=2，CE=
3
，则AF的长为（　　）
A．
2
3
3
B．
21
+1
3
C．
21
+3
3
D．
21
-3
3
如图，外切于P点的⊙O1和⊙O2是半径为3cm的等圆，连心线交⊙O1于点A，交⊙O2于点B，AC与⊙O2相切于点C，连接PC，则PC的长为（　　）
A．2
3
cm		B．3
2
cm		C．3cmD．4.5cm
以平面直角坐标系中的两点O1（0，3）和O2（4，0）为圆心，以8和3为半径的两圆的位置关系是（　　）
A．内切B．外切C．相离D．相交
如图，⊙O1、⊙O2、⊙O3、⊙O4的半径都为1，其中⊙O1与⊙O2外切，⊙O2、⊙O3、⊙O4两两外切，并且O1、O2、O3三点在同一直线上．则：
（1）O2O4的长为______；
（2）若⊙O1沿图中箭头所示方向在⊙O2的圆周上滚动，到第一次与⊙O4重合的位置终止，在上述滚动过程中圆心O1移动的路径长为______．
如图，两枚大小相同的硬币，一枚固定不动，另一枚绕其边缘滚动（无滑动），当运动硬币滚动到原来位置（第一次重合）时，运动硬币自转了（　　）圈．
A．1B．2C．3D．4
已知相交两圆的半径分别为5cm和4cm，公共弦长为6cm，则这两个圆的圆心距是______cm．
如图，相等两圆交于A、B两点，过B任作一直线交两圆于M、N，过M、N各引所在圆的切线相交于C，则四边形AMCN有下面关系成立（　　）
A．有内切圆无外接圆
B．有外接圆无内切圆
C．既有内切圆，也有外接圆
D．以上情况都不对
正方形ABCD的边长是6，分别以A，D为圆心，6为半径在正方形内作弧，圆O与AB，弧BD，弧AC都相切，求圆O的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网