题目内容
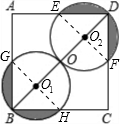
如图，在正方形ABCD中，AB=4，0为对角线BD的中点，分别以OB，OD为直径作⊙O1，⊙02，则图中阴影部分的面积=______．
连接EF、GH，
∵AB=4，
∴BD=
=
=4
，
∵0为对角线BD的中点，
∴O1B=O2B=
=
，
∴⊙O1与⊙O2是半径相等的两个圆，
∵∠EDF=∠GBH=90°，
∴EF、GH分别是⊙O1与⊙O2的直径，
∴S阴影=S⊙O1-2S△DEF
=S⊙O1-2S△DEF
=S⊙O1-2S△GBH
=（
）2π-2×
×2
×
=2π-4．
∵AB=4，
∴BD=
| AD2+AB2 |
| 42+42 |
| 2 |
∵0为对角线BD的中点，
∴O1B=O2B=
4
| ||
| 4 |
| 2 |
∴⊙O1与⊙O2是半径相等的两个圆，
∵∠EDF=∠GBH=90°，
∴EF、GH分别是⊙O1与⊙O2的直径，
∴S阴影=S⊙O1-2S△DEF
=S⊙O1-2S△DEF
=S⊙O1-2S△GBH
=（
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
=2π-4．
练习册系列答案
阅读快车系列答案
相关题目
