题目内容
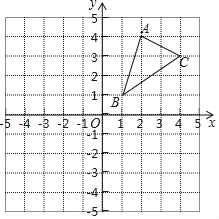
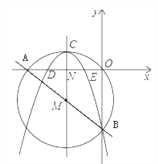
【题目】如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).
(1)求经过B、C、D三点的抛物线对应的函数表达式;
(2)设抛物线的顶点为E,证明:直线CE与⊙A相切.
【答案】(1)y=![]() x2+
x2+![]() x+4;(2)详见解析.
x+4;(2)详见解析.
【解析】
(1)把B(0,4),C(﹣2,0),D(﹣8,0)代入二次函数的解析式即可得到结果;
(2)由y![]() x2
x2![]() x+4
x+4![]() (x+5)2
(x+5)2![]() ,得到顶点坐标E(﹣5,
,得到顶点坐标E(﹣5,![]() ),求得直线CE的函数解析式y
),求得直线CE的函数解析式y![]() ,在y
,在y![]() 中,令x=0,y
中,令x=0,y![]() ,得到G(0,
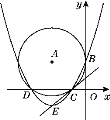
,得到G(0,![]() ),如图1,连接AB,AC,AG,得BG=OB﹣OG=4
),如图1,连接AB,AC,AG,得BG=OB﹣OG=4![]() ,CG
,CG![]() ,得到BG=CG,AB=AC,证得△ABG≌△ACG,得到∠ACG=∠ABG,由于⊙A与y轴相切于点B(0,4),于是得到∠ABG=90°,即可求得结论.
,得到BG=CG,AB=AC,证得△ABG≌△ACG,得到∠ACG=∠ABG,由于⊙A与y轴相切于点B(0,4),于是得到∠ABG=90°,即可求得结论.
(1)设抛物线的解析式为:y=ax2+bx+c,把B(0,4),C(﹣2,0),D(﹣8,0)代入得: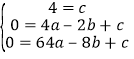 ,解得:
,解得:![]() ,∴经过B,C,D三点的抛物线的函数表达式为:y
,∴经过B,C,D三点的抛物线的函数表达式为:y![]() x2
x2![]() x+4;
x+4;
(2)∵y![]() x2
x2![]() x+4
x+4![]() (x+5)2
(x+5)2![]() ,∴E(﹣5,
,∴E(﹣5,![]() ),设直线CE的函数解析式为y=mx+n,直线CE与y轴交于点G,则
),设直线CE的函数解析式为y=mx+n,直线CE与y轴交于点G,则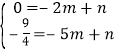 ,解得:
,解得: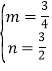 ,∴y
,∴y![]() ,在y
,在y![]() 中,令x=0,y
中,令x=0,y![]() ,∴G(0,
,∴G(0,![]() ),如图1,连接AB,AC,AG,则BG=OB﹣OG=4
),如图1,连接AB,AC,AG,则BG=OB﹣OG=4![]() ,CG
,CG![]() ,∴BG=CG,AB=AC.在△ABG与△ACG中,∵
,∴BG=CG,AB=AC.在△ABG与△ACG中,∵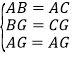 ,∴△ABG≌△ACG,∴∠ACG=∠ABG.
,∴△ABG≌△ACG,∴∠ACG=∠ABG.
∵⊙A与y轴相切于点B(0,4),∴∠ABG=90°,∴∠ACG=∠ABG=90°
∵点C在⊙A上,∴直线CE与⊙A相切.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目