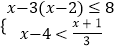��Ŀ����
����Ŀ��Ϊ��ץס�����½���1000����̻���ij�̵��������A��B���������ڼ���Ʒ��������A�ּ���Ʒ8����B�ּ���Ʒ3������Ҫ950Ԫ��������A�ּ���Ʒ5����B�ּ���Ʒ6������Ҫ800Ԫ��
��1����A��B���ּ���Ʒÿ���������Ԫ��
��2�������̵�������������ּ���Ʒ��100���������г�������ʽ���ת�����ڹ�����100������Ʒ���ʽ�����7500Ԫ����������7650Ԫ����ô���̵깲�м��ֽ���������
���𰸡�
��1���⣺����̵깺��һ��A�ּ���Ʒ��ҪaԪ������һ��B�ּ���Ʒ��ҪbԪ��
��������÷�����ã� ![]() ��
��
�ⷽ����ã� ![]() ��
��
���һ��A�ּ���Ʒ��Ҫ100Ԫ������һ��B�ּ���Ʒ��Ҫ50Ԫ��
��2���⣺����̵깺��A�ּ���Ʒx������B�ּ���Ʒ�У�100��x������
�� ![]() ��
��
��ã�50��x��53��
��x ��������x=50��51��52��53
���4�ֽ���������
�ֱ�Ϊ������1���̵깺��A�ּ���Ʒ50������B�ּ���Ʒ��50����
����2���̵깺��A�ּ���Ʒ51������B�ּ���Ʒ��49����
����3���̵깺��A�ּ���Ʒ52������B�ּ���Ʒ��48����
����4���̵깺��A�ּ���Ʒ53������B�ּ���Ʒ��47����
����������1������̵깺��һ��A�ּ���Ʒ��ҪaԪ������һ��B�ּ���Ʒ��ҪbԪ��Ȼ������A�ּ���Ʒ8����ҪǮ��+B�ּ���Ʒ3��Ǯ��=950��A�ּ���Ʒ5����ҪǮ��+B�ּ���Ʒ6����ҪǮ��=800�з�������⼴�ɣ�
��2������̵깺��A�ּ���Ʒx������B�ּ���Ʒ�У�100��x������Ȼ�����ݹ�����100������Ʒ���ʽ�����7500Ԫ����������7650Ԫ�в���ʽ����⼴��.
�����㾫��������һԪһ�β���ʽ���Ӧ�ö���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д������𰸣�