题目内容
如图①,在Rt△ABC中,∠BAC=90°,AB=AC= ,D、E两点分别在AC、BC上,且DE∥AB,CD=
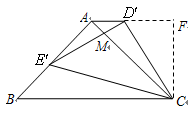
,D、E两点分别在AC、BC上,且DE∥AB,CD=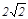 .将△CDE绕点C顺时针旋转,得到△CD’E’(如图②,点D’、E’分别与点D、E对应),点E’在AB上,D’E’与AC相交于点M.
.将△CDE绕点C顺时针旋转,得到△CD’E’(如图②,点D’、E’分别与点D、E对应),点E’在AB上,D’E’与AC相交于点M.

(1)求∠ACE’的度数;
(2)求证:四边形ABCD’是梯形;
(3)求△AD’M的面积.
 ,D、E两点分别在AC、BC上,且DE∥AB,CD=
,D、E两点分别在AC、BC上,且DE∥AB,CD=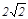 .将△CDE绕点C顺时针旋转,得到△CD’E’(如图②,点D’、E’分别与点D、E对应),点E’在AB上,D’E’与AC相交于点M.
.将△CDE绕点C顺时针旋转,得到△CD’E’(如图②,点D’、E’分别与点D、E对应),点E’在AB上,D’E’与AC相交于点M.
(1)求∠ACE’的度数;
(2)求证:四边形ABCD’是梯形;
(3)求△AD’M的面积.
(1) 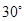 (2)证明见解析(3)
(2)证明见解析(3) 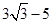
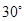 (2)证明见解析(3)
(2)证明见解析(3) 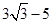
(1)如图1,
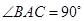 ,
,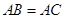 ,
,
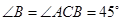 ,
,
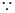
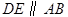 ,
,
 ,
,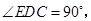

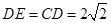 ,
,
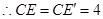 .····························· 1分
.····························· 1分
如图2,在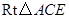 中,
中,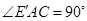 ,
,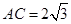 ,
,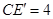 ,
,
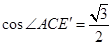 ,
,
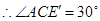 .······························ 3分
.······························ 3分
(2)如图2,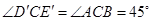 ,
,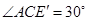 ,
,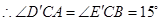 ,
,
又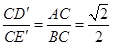 .
.
 .················· 5分
.················· 5分

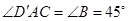 ,
,

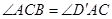 ,
,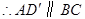 .····················· 7分
.····················· 7分
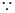
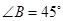 ,
,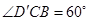 ,
,
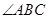 与
与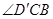 不互补,
不互补,
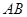 与
与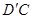 不平行.
不平行.
 四边形
四边形 是梯形.·························· 8分
是梯形.·························· 8分
(3)在图2中,过点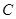 作
作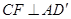 ,垂足为
,垂足为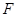 .
.
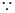
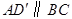 ,
,
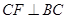 .
.

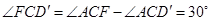 .
.
在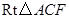 中,
中,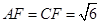 ,
,
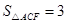 ,
,
在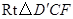 中,
中,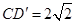 ,
,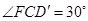 ,
,

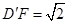 ,
,
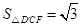 .
.
同理,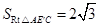 ,
,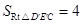 .··················· 10分
.··················· 10分
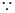
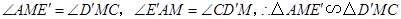 .
.
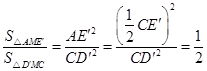 .······················ 11分
.······················ 11分
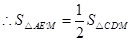 . (1)
. (1)
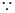
 , (2)
, (2)
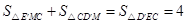 . (3)
. (3)
(3)-(2),得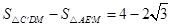 ,由(1),得
,由(1),得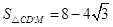 ,
,

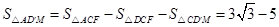 .
.

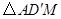 的面积是
的面积是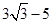 .
.
(1)根据两直线平行,同位角相等,可知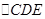 是等腰直角三角形,在
是等腰直角三角形,在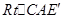 中,算出
中,算出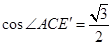 ,即
,即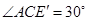
(2)找出三角形相似的条件,利用相似三角形的对应角相等,内错角相等两直线平行及一组边平行,另一组边不平行的四边形是梯形
(3)利用补的方法求△AD’M的面积,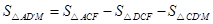 ,用解直角三角形算出一些边长,利用相似三角形面积比等于相似比的平方,算出三角形面积即可
,用解直角三角形算出一些边长,利用相似三角形面积比等于相似比的平方,算出三角形面积即可
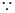
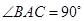 ,
,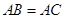 ,
,
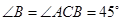 ,
,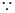
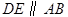 ,
,
 ,
,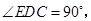

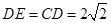 ,
,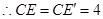 .····························· 1分
.····························· 1分如图2,在
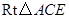 中,
中,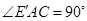 ,
,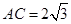 ,
,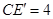 ,
,
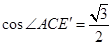 ,
,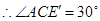 .······························ 3分
.······························ 3分(2)如图2,
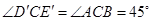 ,
,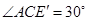 ,
,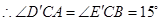 ,
,又
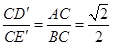 .
.
 .················· 5分
.················· 5分
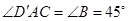 ,
,
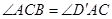 ,
,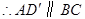 .····················· 7分
.····················· 7分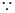
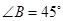 ,
,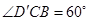 ,
,
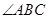 与
与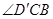 不互补,
不互补,
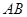 与
与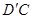 不平行.
不平行. 四边形
四边形 是梯形.·························· 8分
是梯形.·························· 8分(3)在图2中,过点
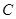 作
作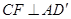 ,垂足为
,垂足为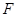 .
.
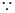
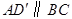 ,
,
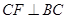 .
.
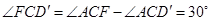 .
.在
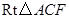 中,
中,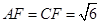 ,
,
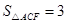 ,
, 在
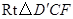 中,
中,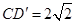 ,
,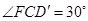 ,
,
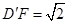 ,
,
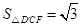 .
.同理,
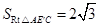 ,
,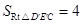 .··················· 10分
.··················· 10分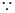
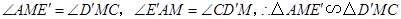 .
.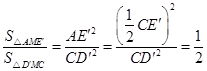 .······················ 11分
.······················ 11分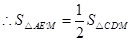 . (1)
. (1)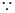
 , (2)
, (2)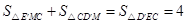 . (3)
. (3)(3)-(2),得
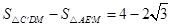 ,由(1),得
,由(1),得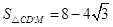 ,
,
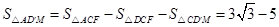 .
.
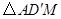 的面积是
的面积是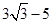 .
.(1)根据两直线平行,同位角相等,可知
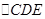 是等腰直角三角形,在
是等腰直角三角形,在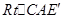 中,算出
中,算出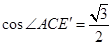 ,即
,即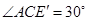
(2)找出三角形相似的条件,利用相似三角形的对应角相等,内错角相等两直线平行及一组边平行,另一组边不平行的四边形是梯形
(3)利用补的方法求△AD’M的面积,
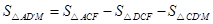 ,用解直角三角形算出一些边长,利用相似三角形面积比等于相似比的平方,算出三角形面积即可
,用解直角三角形算出一些边长,利用相似三角形面积比等于相似比的平方,算出三角形面积即可
练习册系列答案
相关题目

 中
中 ,
, ,
, .
.
 个单位长度,画出平移后的
个单位长度,画出平移后的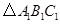 ;
;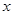 轴对称的
轴对称的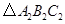 ;
;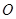 旋转
旋转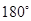 ,画出旋转后的
,画出旋转后的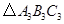 ;
; ______与
______与
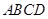 与
与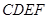 ,旋转长方形
,旋转长方形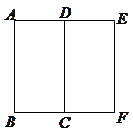
 中,
中, 为
为 边的中点,
边的中点,
 绕
绕 点旋转,它的两边分别交
点旋转,它的两边分别交 、
、 (或它们的延长线)于
(或它们的延长线)于 、
、
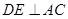 于
于
 不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立, 、
、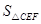 、
、 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
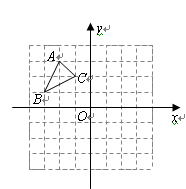
 绕点
绕点 逆时针旋转
逆时针旋转 ,得到
,得到 .若点
.若点 的坐标为
的坐标为 ,则点
,则点 的坐标为 .
的坐标为 .
