题目内容
矩形ABCD的边长AB=6，BC=4，点F在DC上，DF=2．动点M、N分别从点D、B同时出发，沿线段DA、线段BA向点A的方向运动，当动点M运动到点A时，M、N两点同时停止运动．连接FM、FN．设点M、N的运动速度都是1个单位/秒，M、N运动的时间为x秒，问：当x为多少时，FM⊥FN？
分析：首先构造直角三角形，用x表示出各部分的长度，再结合勾股定理求出x的值．
解答：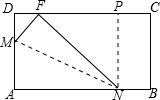
解：连接MN，做NP⊥DC，
当FM⊥FN时，即△MFN为直角三角形，
∴FM2+FN2=MN2，
∵MN2=AM2+AN2，
DM2+DF2=FM2，PF2+PN2=FN2，
又∵设点M、N的运动速度都是1个单位/秒，矩形ABCD的边长AB=6，BC=4，DF=2，M、N运动的时间为x秒，DM=x，AM=4-x，AN=6-x，PN=4，PF=6-2-x，
∴DM2+DF2+PF2+PN2=AM2+AN2，
∴x2+4+（4-x）2+16=（4-x）2+（6-x）2，
解得：x=
，
∴当x为
时FM⊥FN．
解：连接MN，做NP⊥DC，当FM⊥FN时，即△MFN为直角三角形，
∴FM2+FN2=MN2，
∵MN2=AM2+AN2，
DM2+DF2=FM2，PF2+PN2=FN2，
又∵设点M、N的运动速度都是1个单位/秒，矩形ABCD的边长AB=6，BC=4，DF=2，M、N运动的时间为x秒，DM=x，AM=4-x，AN=6-x，PN=4，PF=6-2-x，
∴DM2+DF2+PF2+PN2=AM2+AN2，
∴x2+4+（4-x）2+16=（4-x）2+（6-x）2，
解得：x=
| 4 |
| 3 |
∴当x为
| 4 |
| 3 |
点评：此题主要考查了勾股定理的应用，以及动点问题，解决问题的关键是得出个部分线段的长度．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
如图，矩形ABCD的边长AB=9，AD=3，将此矩形置于平面直角坐标系xOy中，使AB在x轴正半轴上，经过点C的直线
如图，矩形ABCD的边长AB=1，AD=
如图，已知矩形ABCD的边长AB=3cm，BC=6cm，某一时刻，动点M从点A出发沿AB方向以1cm∕s的速度向点B匀速运动；同时，动点N从点D沿DA方向以2cm∕s的速度向点A匀速运动．经过多少时间，△AMN的面积等于矩形ABCD面积的
如图，矩形ABCD的边长AB=4，BC=2，则在边CD上，存在（ ）个点P，使∠APB=90°．