题目内容
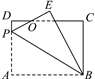
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
【答案】
(1)证明:∵PQ垂直平分BE,
∴QB=QE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,
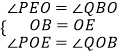 ,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(2)解:∵O,F分别为PQ,AB的中点,
∴AE+BE=2OF+2OB=18,
设AE=x,则BE=18﹣x,
在Rt△ABE中,62+x2=(18﹣x)2,
解得x=8,
BE=18﹣x=10,
∴OB= ![]() BE=5,
BE=5,
设PE=y,则AP=8﹣y,BP=PE=y,
在Rt△ABP中,62+(8﹣y)2=y2,解得y= ![]() ,
,
在Rt△BOP中,PO= ![]() =
= ![]() ,
,
∴PQ=2PO= ![]() .
.
【解析】(1)先根据线段垂直平分线的性质证明QB=QE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形ABGE是平行四边形,得到QB=QE,再根据菱形的判定即可得出四边形BPEQ是菱形;
(2)根据三角形中位线的性质可得AE+BE=2OF+2OB=18,设AE=x,则BE=18-x,在Rt△ABE中,根据勾股定理可得62+x2=(18-x)2,BE=10,得到OB=5,再勾股定理求出y和PO的值即可PQ的长.
【考点精析】通过灵活运用线段垂直平分线的性质和矩形的性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.