题目内容
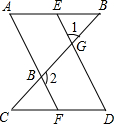如图，已知：∠1与∠2互补，∠A=∠D，求证：AB∥CD．
证明：∵∠1=∠CGD，∠1与∠2互补，
∴∠CGD+∠2=180°，
∴AF∥ED，
∴∠A+∠AED=180°，
∵∠A=∠D，
∴∠D+∠AED=180°，
∴AB∥CD．
分析：由对顶角相等得到一对角相等，根据已知一对角互补，得到同旁内角互补，利用同旁内角互补两直线平行得到AF与ED平行，由两直线平行同旁内角互补得到一对角互补，等量代换得到∠D与∠AED互补，利用同旁内角互补两直线平行即可得证．
点评：此题考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．
∴∠CGD+∠2=180°，
∴AF∥ED，
∴∠A+∠AED=180°，
∵∠A=∠D，
∴∠D+∠AED=180°，
∴AB∥CD．
分析：由对顶角相等得到一对角相等，根据已知一对角互补，得到同旁内角互补，利用同旁内角互补两直线平行得到AF与ED平行，由两直线平行同旁内角互补得到一对角互补，等量代换得到∠D与∠AED互补，利用同旁内角互补两直线平行即可得证．
点评：此题考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
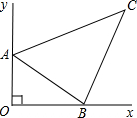如图，已知射线ox与射线oy互相垂直，B，A分别为ox、oy上一动点，∠ABx、∠BAy的平分线交于C．问：B、A在ox、oy上运动过程中，∠C的度数是否改变？若不改变，求出其值；若改变，说明理由．
20、如图，已知线段AB与P、Q两点，
交于A、B两点（点A在点B的左侧）．
如图，已知：AC与BD交于点E，AB=BC，AC=BD． 求证：△ADE≌△BCE．
如图，已知弦AB与半径相等，连接OB，并延长使BC=OB．