题目内容
 如图,已知弦AB与半径相等,连接OB,并延长使BC=OB.
如图,已知弦AB与半径相等,连接OB,并延长使BC=OB.(1)问AC与⊙O有什么关系.并证明你的结论的正确性.
(2)请你在⊙O上找出一点D,使AD=AC(自己完成作图,并证明你的结论).
分析:(1)连接OA,由OA=OB=AB,BC=OB,可得AB=BC,根据等边对等角,即可得∠O=∠OAB,∠C=∠CAB,又由三角形内角和定理,可求得∠OAC=90°,即可证得AC是⊙O的切线;
(2)延长BO交⊙O于D,连接AD,则AD即为所求;由OA=OB=AB,可求得∠AOB=60°,继而可得∠C=30°,又由圆周角定理,求得∠D=30°,然后根据等角对等边,即可证得AD=AC.
(2)延长BO交⊙O于D,连接AD,则AD即为所求;由OA=OB=AB,可求得∠AOB=60°,继而可得∠C=30°,又由圆周角定理,求得∠D=30°,然后根据等角对等边,即可证得AD=AC.
解答: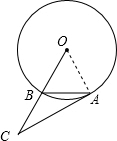 解:(1)AC是⊙O的切线.
解:(1)AC是⊙O的切线.
证明:连接OA,
∵OA=OB=AB,
∴∠OBA=∠OAB=∠O,
∵BC=OB,
∴BC=AB,
∴∠C=∠CAB,
∵∠O+∠C+∠OAC=180°,
即∠O+∠OAB+∠CAB+∠C=180°,
∴∠OAC=∠OAB+∠CAB=90°,
即OA⊥AC,
∴AC是⊙O的切线;
(2)延长BO交⊙O于D,连接AD,则AD即为所求.
理由:∵OB=OA=AB,
∴∠AOB=60°,
∵∠OAC=90°,
∴∠C=90°-∠AOB=30°,
∵∠D=
∠AOB=30°,
∴∠D=∠C,
∴AC=AD.
 解:(1)AC是⊙O的切线.
解:(1)AC是⊙O的切线.证明:连接OA,
∵OA=OB=AB,
∴∠OBA=∠OAB=∠O,
∵BC=OB,
∴BC=AB,
∴∠C=∠CAB,
∵∠O+∠C+∠OAC=180°,
即∠O+∠OAB+∠CAB+∠C=180°,
∴∠OAC=∠OAB+∠CAB=90°,
即OA⊥AC,
∴AC是⊙O的切线;
(2)延长BO交⊙O于D,连接AD,则AD即为所求.
理由:∵OB=OA=AB,

∴∠AOB=60°,
∵∠OAC=90°,
∴∠C=90°-∠AOB=30°,
∵∠D=
| 1 |
| 2 |
∴∠D=∠C,
∴AC=AD.
点评:此题考查了切线的判定与性质、圆周角定理、等边三角形的判定与性质、等腰三角形的判定与性质等知识.此题综合性较强,难度适中,解题的关键是注意准确作出辅助线,注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

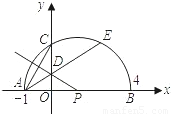
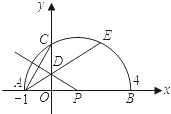 两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.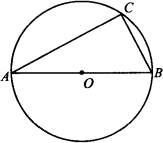
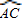 与
与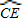 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.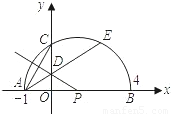
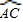 与
与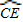 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.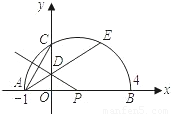
 与
与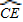 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.