��Ŀ����
����Ŀ������C=������EAC+��FBC=��
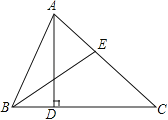
��1����ͼ����AM�ǡ�EAC��ƽ���ߣ�BN�ǡ�FBC��ƽ���ߣ���AM��BN�����������кι�ϵ����˵�����ɣ�
��2����ͼ�ڣ�����EAC��ƽ��������ֱ�����FBCƽ��������ֱ�߽���P����̽����APB���������Ĺ�ϵ��______��������������ʾ��
��3����ͼ�ۣ������ݦ�����EAC���FBC��ƽ�����ཻ��P1����EAP1���FBP1��ƽ���߽���P2 ���������ƣ����P5=______��������������ʾ��
 ��
�� ��
��
���𰸡� ��APB=����![]() �� ��P5=����
�� ��P5=����![]() ��
��
�������������������1�����ݽ�ƽ���ߵĶ����ʾ����MAC����NCB���ٸ�����ֱ��ƽ�У��ڴ�����ȿɵá�C����MAC����NBC��
��2�����ݽ�ƽ���ߵĶ����ʾ����PAC����PBC�����������ε�һ����ǵ������������ڵ������ڽǵĺ���ʽ�������ɵý⣻
��3�����ݣ�2���Ľ��۷ֱ��ʾ����P1����P2�����Ӷ��ý⣮
���������
�⣺��1����AM�ǡ�EAC��ƽ���ߣ�BN�ǡ�FBC��ƽ���ߣ�
���MAC����NCB��![]() ��EAC��
��EAC��![]() ��FBC��
��FBC��![]() ����
����
��AM��BN��
���C����MAC����NCB��
������![]() ����
����
��2���ߡ�EAC��ƽ�������FBCƽ�����ཻ��P��
���PAC����PBC��![]() ��EAC��
��EAC��![]() ��FBC��
��FBC��![]() ����
����
���C����APB������PAC����PBC����
��������APB��![]() ����
����
����APB������![]() ����
����
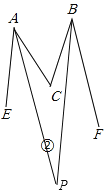
��3���ɣ�2���ã���P1����C������PAC����PBC��������![]() ����
����
��P2����P1������P2AP1����P2BP1����
������![]() ����
����![]() ��������
��������![]() ����
����
��P3������![]() ����
����![]() ��������
��������![]() ����
����
��P4������![]() ����
����![]() ��������
��������![]() ����
����
��P5������![]() ����
����![]() ��������
��������![]() ����
����

 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�