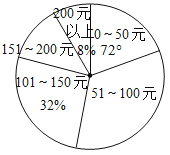
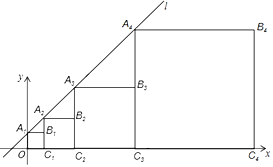
��Ŀ����
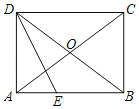
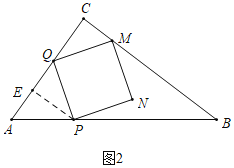
����Ŀ����ͼ����Rt��ABC�У���C=90����AB=10��AC=6������P��Q�ӵ�Aͬʱ��������P��ÿ��5����λ���ٶ��ر�AB���յ�B�����˶�����Q������AC��CB���յ�B�����˶�����AC��CB�ϵ��ٶȷֱ���ÿ��6����λ��ÿ��8����λ����PQΪ����������PQMN��ʹ�õ�M���Cʼ����PQ��ͬ�࣮���P�˶���ʱ��Ϊt��s����
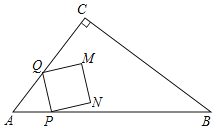
��1������Q�ڱ�AC��ʱ���ú�t�Ĵ���ʽ��ʾPQ�ij���
��2������M���ڱ�BC��ʱ����t��ֵ��
��3������Q�ڱ�AC��ʱ����������PQMN����ABC�ص�����ͼ�ε����ΪS����S��t֮��ĺ�����ϵʽ��
��4����������PQMN�ı�QM����ABC�ı�ƽ��ʱ��ֱ��д��t��ֵ��
���𰸡���1��PQ =5t����2������M����BC��ʱ��t��ֵΪ![]() ����3��S=25t2��
����3��S=25t2��![]() ��
��![]() ����4������������t��ֵΪ
����4������������t��ֵΪ![]() ��
��![]() ��
��
��������
��1����ͼ1�У���PE��AC��E��֤��PQ��PA���ɽ�����⣮
��2����ͼ2�У�֤����MQC����B������cos��MQC��cos��B���������̼��ɽ�����⣮
��3�����������Σ�����0��t��![]() ʱ���ص�������������PQMN������
ʱ���ص�������������PQMN������![]() ��t��
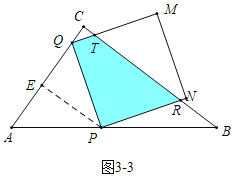
��t��![]() ʱ����ͼ3��2�У��ص������������PQTRN������
ʱ����ͼ3��2�У��ص������������PQTRN������![]() ��t��1ʱ���ص��������ı���PQTR���ֱ���⼴�ɽ�����⣮
��t��1ʱ���ص��������ı���PQTR���ֱ���⼴�ɽ�����⣮
��4�����������Σ�����ͼ4��1�У���QT��TMʱ����cos��CQT��![]() ���������̼��ɽ�����⣮����ͼ4��2�У���MT��TQʱ����sin��CTQ��
���������̼��ɽ�����⣮����ͼ4��2�У���MT��TQʱ����sin��CTQ��![]() ���������̼��ɽ�����⣮
���������̼��ɽ�����⣮
�⣺��1����ͼ1�У���PE��AC��E��
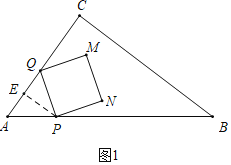
��Rt��ABC����AB=10��AC=6��
��![]() ��
��
�ߡ�PEA=��C=90����
��PE��BC��
��![]() ��
��
��![]() ��
��
��AE=3t��
��AQ=6t��
��AE=EQ=3t��
��PE��ֱƽ���߶�AQ��
��PQ=PA=5t��
��2����ͼ2�У�����M����BC��ʱ��
���ı���PQMN�������Σ�
��MQ=PQ=5t����MQP=90����
���AQP+��MQC=90�����ߡ�A+��B=90������A=��AQP��
���MQC=��B��
��cos��MQC=cos��B��
��![]() ��
��
��![]() ��
��
���![]() ��
��
������M����BC��ʱ��t��ֵΪ![]() ��
��
��3������![]() ʱ���ص�������������PQMN��S=25t2��
ʱ���ص�������������PQMN��S=25t2��
������N����BC��ʱ����ͼ3-1�У���QG��AB��G��NH��AB��H������QGP�ա�HPN��AAS�����ɵ�QG=PH��PG=NH��
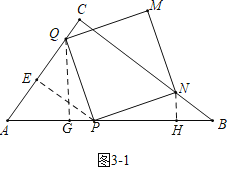
��![]() ��
��
��![]() ��
��
��![]() ��
��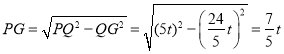 ��
��
��![]() ��
��
��![]() ��
��
���![]() ��
��
����![]() ʱ����ͼ3-2�У��ص������������PQTRN��
ʱ����ͼ3-2�У��ص������������PQTRN��
![]()
![]() ��
��
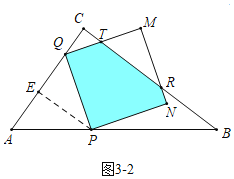
����![]() ʱ���ص��������ı���PQTR��
ʱ���ص��������ı���PQTR��
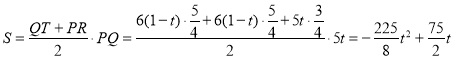 ��
��
��4����ͼ4-1�У���QT=TMʱ����![]() ���ɵ�
���ɵ�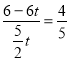 �����
�����![]() ��
��
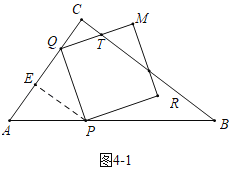
��ͼ4-2�У���MT=TQʱ����![]() ���ɵ�
���ɵ�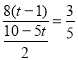 �����
�����![]() ��
��
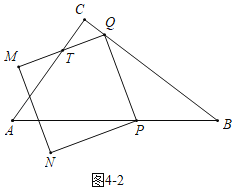
��������������������t��ֵΪ![]() ��
��![]() ��
��