题目内容
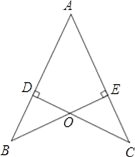
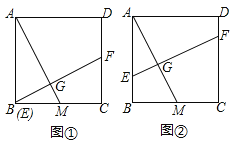
【题目】如图,正方形ABCD,AB=4,点M是边BC的中点,点E是边AB上的一个动点,作EG⊥AM交AM于点G,EG的延长线交线段CD于点F.
(1)如图①,当点E与点B重合时,求证:BM=CF;
(2)设BE=x,梯形AEFD的面积为y,求y与x的函数解析式,并写出定义域.
【答案】(1)见解析;(2)y与x的函数解析式为![]() .
.
【解析】
(1)证明△BAM≌△CBF,根据全等三角形的性质证明;
(2)作EH⊥CD于H,根据全等三角形的性质求出FH,再根据梯形的面积公式计算即可.
(1)证明:∵GE⊥AM,∴∠BAM+∠ABG=90°,又∠CBF+∠ABG=90°,
在△BAM和△CBF中,∠BAM=∠CBF,AB=BC,∠ABM=∠BCF,
∴△BAM≌△CBF(ASA),∴BM=CF;

(2)解:作EH⊥CD于H,由(1)得:△BAM≌△HEF,
∴HF=BM=2,∴DF=4-2-x=2-x,
∴![]() ,
,
答:y与x的函数解析式为![]() .
.
故答案为:(1)见解析;(2)y与x的函数解析式为![]() .
.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目