题目内容
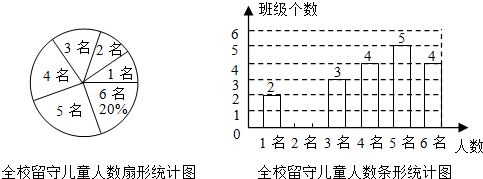
(2013•沐川县二模)为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图:
(1)将该条形统计图补充完整;
(2)求该校平均每班有多少名留守儿童?
(3)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
(1)将该条形统计图补充完整;
(2)求该校平均每班有多少名留守儿童?
(3)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.

分析:(1)根据留守儿童有6名的班级占20%,可求得有留守儿童的总班级数,再减去其它班级数,即可补全统计图;
(2)根据班级个数和班级人数,求出总的留守儿童数,再除以总班级数,即可得出答案;
(3)根据(1)可知,只有2名留守儿童的班级有2个,共4名学生,再设A1,A2来自一个班,B1,B2来自一个班,列出树状图可得出来自一个班的共有4种情况,再根据概率公式即可得出答案.
(2)根据班级个数和班级人数,求出总的留守儿童数,再除以总班级数,即可得出答案;
(3)根据(1)可知,只有2名留守儿童的班级有2个,共4名学生,再设A1,A2来自一个班,B1,B2来自一个班,列出树状图可得出来自一个班的共有4种情况,再根据概率公式即可得出答案.
解答:解:(1)该校班级个数为4÷20%=20(个),
只有2名留守儿童的班级个数为:20-(2+3+4+5+4)=2(个),
补图如下:

(2)该校平均每班留守儿童的人数为:
(1×2+2×2+3×3+4×4+5×5+6×4)÷20=4(个);
(3)由(1)得只有2名留守儿童的班级有2个,共4名学生,设A1,A2来自一个班,B1,B2来自一个班,如图;

由树状图可知,共有12种可能的情况,并且每种结果出现的可能性相等,其中来自一个班的共有4种情况,
则所选两名留守儿童来自同一个班级的概率为:
=
.
只有2名留守儿童的班级个数为:20-(2+3+4+5+4)=2(个),
补图如下:

(2)该校平均每班留守儿童的人数为:
(1×2+2×2+3×3+4×4+5×5+6×4)÷20=4(个);
(3)由(1)得只有2名留守儿童的班级有2个,共4名学生,设A1,A2来自一个班,B1,B2来自一个班,如图;

由树状图可知,共有12种可能的情况,并且每种结果出现的可能性相等,其中来自一个班的共有4种情况,
则所选两名留守儿童来自同一个班级的概率为:
| 4 |
| 12 |
| 1 |
| 3 |
点评:本题考查了条形统计图和扇形统计图以及及树状图的画法,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
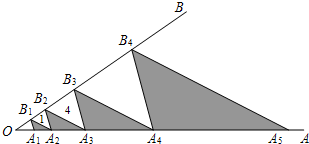 (2013•沐川县二模)如图,点A1,A2,A3,A4,…,An在射线OA上,点B1,B2,B3,…,Bn-1在射线OB上,且A1B1∥A2B2∥A3B3∥…∥An-1Bn-1,A2B1∥A3B2∥A4B3∥…∥AnBn-1,△A1A2B1,△A2A3B2,…,△An-1AnBn-1为阴影三角形,若△A2B1B2,△A3B2B3的面积分别为1、4,则△A1A2B1的面积为
(2013•沐川县二模)如图,点A1,A2,A3,A4,…,An在射线OA上,点B1,B2,B3,…,Bn-1在射线OB上,且A1B1∥A2B2∥A3B3∥…∥An-1Bn-1,A2B1∥A3B2∥A4B3∥…∥AnBn-1,△A1A2B1,△A2A3B2,…,△An-1AnBn-1为阴影三角形,若△A2B1B2,△A3B2B3的面积分别为1、4,则△A1A2B1的面积为