Question

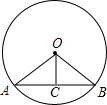
如图，⊙C经过坐标原点，并与坐标轴分别交于A、D两点，点B在⊙C上，∠B=30°，点D的坐标为（0，2），求A、C两点的坐标．

Answer 1

连接AC、OC，过点C分别作CM⊥OD于M，CN⊥OA于N．
∵点B在⊙C上，∠B=30°，
∴∠ACO=60°．
∵CA=CO，
∴△CAO是等边三角形．
∴CA=CO=OA，∠COA=60°．
∴∠COM=30°．
∵CM⊥OD，点C为圆心，点D的坐标为（0，2），
∴OM=

1

2

OD=1．
在Rt△OCM中，CM=

1

2

OC，
由勾股定理得，OC=

2 3

3

．
∴OA=

2 3

3

．
同理可得CN=1，ON=

3

3

．
∴点A的坐标为(-

2 3

3

，0)．
点C的坐标为(-

3

3

，1)．