题目内容
如图,已知∠xoy=90°,线段AB=10,若点A在oy上滑动,点B随着线段AB在射线o x上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.
x上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.(1)在上述变化过程中:Rt△AOB的周长,⊙K的半径,△AOB外接圆半径,这几个量中不会发生变化的是什么?并简要说明理由;
(2)当AE=4时,求⊙K的半径r;
(3)当Rt△AOB的面积为S,AE为x,试求:S与x之间的函数关系,并求出S最大时直角边OA的长.
分析:(1)根据直角三角形的性质,斜边上的中线等于斜边的一半,AB的长不变,即△AOB的外接圆半径不变;
(2)设⊙K的半径为r,连EK、KF,则四边形EOFK是正方形,根据切线长定理,可求得r;
(3)设AO=b,OB=a,可得出r=
,即2(b-x)+10=a+b,再由S=
ab,则S=-x2+10x.再求得该函数的顶点坐标的横坐标.
(2)设⊙K的半径为r,连EK、KF,则四边形EOFK是正方形,根据切线长定理,可求得r;
(3)设AO=b,OB=a,可得出r=
| a+b-10 |
| 2 |
| 1 |
| 2 |
解答: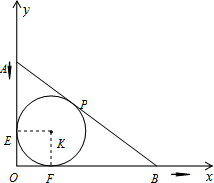 解:(1)不会发生变化的是△AOB的外接圆半径,
解:(1)不会发生变化的是△AOB的外接圆半径,
∵∠AOB=90°,
∴AB是△AOB的外接圆的直径
AB的长不变,即△AOB的外接圆半径不变
(2)设⊙K的半径为r,⊙K与Rt△AOB相切于E、F、P,连EK、KF
∴∠KEO=∠OFK=∠O=90°,
∴四边形EOFK是矩形,
又∵OE=OF
∴四边形EOFK是正方形,
∴OE=OF=r,AE=AP=4,
∴PB=BF=6,
∴(4+r)2+(6+r)2=100,
∴r=-12(不符合题意),r=2,
(3)设AO=b,OB=a,⊙K与Rt△AOB三边相切于E、F、P,
∴OE=r=
,即2(b-x)+10=a+b,∴10-2x=a-b,
∴100-40x+4x2=a2+b2-2ab,
∵S=
ab,
∴ab=2S,a2+b2=102
∴100-40x+4x2=100-4S,
∴S=-x2+10x,
另一解法:(x+r)2+(10-x+r)2=100,
∴r2+10r=-x2+10x
S=
•r(OA+OB+AB)=
r(r+x+10-x+r+10)=
r(20+2r)=r2+10r
∴S=r2+10r=-x2+10x,
又∵S=-x2+10x=-(x-5)2+25
∵当x=5时,S最大,即AE=BF=5,
∴OA=
=5
.
 解:(1)不会发生变化的是△AOB的外接圆半径,
解:(1)不会发生变化的是△AOB的外接圆半径,∵∠AOB=90°,
∴AB是△AOB的外接圆的直径
AB的长不变,即△AOB的外接圆半径不变
(2)设⊙K的半径为r,⊙K与Rt△AOB相切于E、F、P,连EK、KF
∴∠KEO=∠OFK=∠O=90°,
∴四边形EOFK是矩形,
又∵OE=OF
∴四边形EOFK是正方形,
∴OE=OF=r,AE=AP=4,
∴PB=BF=6,
∴(4+r)2+(6+r)2=100,
∴r=-12(不符合题意),r=2,
(3)设AO=b,OB=a,⊙K与Rt△AOB三边相切于E、F、P,
∴OE=r=
| a+b-10 |
| 2 |
∴100-40x+4x2=a2+b2-2ab,
∵S=
| 1 |
| 2 |
∴ab=2S,a2+b2=102
∴100-40x+4x2=100-4S,
∴S=-x2+10x,
另一解法:(x+r)2+(10-x+r)2=100,
∴r2+10r=-x2+10x
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S=r2+10r=-x2+10x,
又∵S=-x2+10x=-(x-5)2+25
∵当x=5时,S最大,即AE=BF=5,
∴OA=
| 10 | ||
|
| 2 |
点评:本题是一道中考压轴题,考查了二次函数与三角形的内切圆、外接圆的综合题,难度偏大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 23、如图,已知∠XOY=90°,正△PAB的顶点P与O点重合,顶点A是射线OX上的一个定点,另一顶点B在∠XOY的内部.
23、如图,已知∠XOY=90°,正△PAB的顶点P与O点重合,顶点A是射线OX上的一个定点,另一顶点B在∠XOY的内部. (2012•崇左)如图,已知∠XOY=90°,等边三角形PAB的顶点P与O点重合,顶点A是射线OX上的一个定点,另一个顶点B在∠XOY的内部.
(2012•崇左)如图,已知∠XOY=90°,等边三角形PAB的顶点P与O点重合,顶点A是射线OX上的一个定点,另一个顶点B在∠XOY的内部.
