题目内容
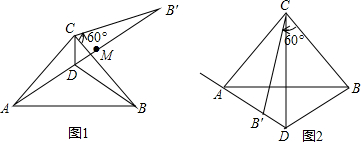 已知:如图,△ABC中,AC=BC,∠ACB=90°,将线段CB绕点C旋转60°得到CB′,∠ACB的平分线CD交直线AB′于点D,连接DB,在射线DB′上截取DM=DC.
已知:如图,△ABC中,AC=BC,∠ACB=90°,将线段CB绕点C旋转60°得到CB′,∠ACB的平分线CD交直线AB′于点D,连接DB,在射线DB′上截取DM=DC.(1)在图1中证明:MB′=DB;
(2)若AC=
| 6 |
分析:(1)连接CM,根据旋转的性质得CB=CB′,∠BCB′=60°,则CA=CB′,∠ACB′=150°,由CD平分∠ACB得∠ACD=∠BCD=45°,∠CDM=60°,利用DM=DC可得到△CDM是等边三角形,所以CM=CD,∠DCM=60°,则可计算出∠B′CM=45°,即∠B′CM=∠BCD,然后根据“SAS”可判断△CBM′≌△CDB,于是得到M′B=BD;
(2)在图1中,作B′H⊥AC交AC的延长线于H,则∠B′CH=30°,在Rt△B′CH中,根据含30度的直角三角形三边的关系得到B′H=
,CH=
B′H=
,则AH=
+
,然后利用勾股定理计算AB′;在图2中,作B′H⊥AC于H,利用同样的方法可求AB′.
(2)在图1中,作B′H⊥AC交AC的延长线于H,则∠B′CH=30°,在Rt△B′CH中,根据含30度的直角三角形三边的关系得到B′H=
| ||
| 2 |
| 3 |
3
| ||
| 2 |
| 6 |
3
| ||
| 2 |
解答: (1)证明:在图1中,连接CM,
(1)证明:在图1中,连接CM,
∵线段CB绕点C旋转60°得到CB′,
∴CB=CB′,∠BCB′=60°,
∵AC=BC,∠ACB=90°,
∴CA=CB′,∠ACB′=90°+60°=150°,
∴∠CAB′=∠B′=15°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°.
∴∠CDM=∠ACD+∠CAD=60°,
∵DM=DC,
∴△CDM是等边三角形,
∴CM=CD,∠DCM=60°,
∴∠B′CM=∠ACB′-∠ACD-∠DCM=45°,
∴∠B′CM=∠BCD,
在△CMB′和△CDB中,
,
∴△CBM′≌△CDB(SAS),
∴M′B=BD;
(2)解:在图1中,作B′H⊥AC交AC的延长线于H,
∵∠ACB′=150°,
∴∠B′CH=30°,
在Rt△B′CH中,CB′=AC=
,
∴B′H=
CB′=
,
CH=
B′H=
,
∴AH=
+
,
在Rt△AB′H中,AB′2=B′H2+AH2=(
)2+(
+
)2=3(
+1)2,
∴AB′=
(
+1)=3+
;
在图2中,作B′H⊥AC于H,
∵∠BCB′=60°,∠ACB=90°,
∴∠B′CH=30°,
在Rt△B′CH中,CB′=AC=
,
∴B′H=
CB′=
,
CH=
B′H=
,
∴AH=
-
,
在Rt△AB′H中,AB′2=B′H2+AH2=(
)2+(
-
)2=3(
-1)2,
∴AB′=
(
-1)=3-
.
 (1)证明:在图1中,连接CM,
(1)证明:在图1中,连接CM,∵线段CB绕点C旋转60°得到CB′,
∴CB=CB′,∠BCB′=60°,
∵AC=BC,∠ACB=90°,
∴CA=CB′,∠ACB′=90°+60°=150°,
∴∠CAB′=∠B′=15°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°.
∴∠CDM=∠ACD+∠CAD=60°,
∵DM=DC,
∴△CDM是等边三角形,
∴CM=CD,∠DCM=60°,
∴∠B′CM=∠ACB′-∠ACD-∠DCM=45°,
∴∠B′CM=∠BCD,
在△CMB′和△CDB中,
|
∴△CBM′≌△CDB(SAS),
∴M′B=BD;
(2)解:在图1中,作B′H⊥AC交AC的延长线于H,
∵∠ACB′=150°,
∴∠B′CH=30°,
在Rt△B′CH中,CB′=AC=
| 6 |
∴B′H=
| 1 |
| 2 |
| ||
| 2 |
CH=
| 3 |
3
| ||
| 2 |
∴AH=
| 6 |
3
| ||
| 2 |
在Rt△AB′H中,AB′2=B′H2+AH2=(
| ||
| 2 |
| 6 |
3
| ||
| 2 |
| 3 |
∴AB′=
| 3 |
| 3 |
| 3 |
在图2中,作B′H⊥AC于H,
∵∠BCB′=60°,∠ACB=90°,
∴∠B′CH=30°,
在Rt△B′CH中,CB′=AC=
| 6 |
∴B′H=
| 1 |
| 2 |
| ||
| 2 |
CH=
| 3 |
3
| ||
| 2 |
∴AH=
| 6 |
3
| ||
| 2 |
在Rt△AB′H中,AB′2=B′H2+AH2=(
| ||
| 2 |
| 6 |
3
| ||
| 2 |
| 3 |
∴AB′=
| 3 |
| 3 |
| 3 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质、等腰直角三角形的性质、全等三角形的判定与性质和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N. 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长. 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE. 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A. 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.