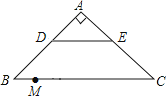题目内容
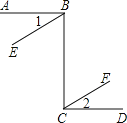
【题目】如图，直线AB和直线CD，直线BE和直线CF都被直线BC所截，在下面三个式子只，请你选择其中两个作为题设，剩下的一个作为结论，组成一个真命题并写出对应的推理过程
题设
已知
；______
结论求证：______
理由：
【答案】
；
【解析】
可以由①②得到③：由于AB∥CD、BE∥CF，利用平行线的性质得到∠ABC=∠DCB，又BE∥CF，则∠EBC=∠FCB，可得到∠ABC-∠EBC=∠DCB-∠FCB，即有∠1=∠2．（答案不唯一）
已知：如图，AB∥CD、BE∥CE，
求证：∠1=∠2．
证明：如图，
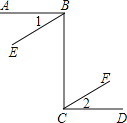
∵AB∥CD，
∴∠ABC=∠DCB，
又∵BE∥CF，
∴∠EBC=∠FCB，
∴∠ABC-∠EBC=∠DCB-∠FCB，
∴∠1=∠2．
【题目】如图，在四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折得到△FMN，若MF∥AD，FN∥DC，则∠D的度数为( )
A. 115° B. 105° C. 95° D. 85°
【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”，下面我们来探究两类特殊的勾股数．通过观察完成下面两个表格中的空格（以下a、b、c为Rt△ABC的三边，且a＜b＜c）：
表一
a | b | c |
3 | 4 | 5 |
5 | 12 | 13 |
7 | 24 | 25 |
9 | 41 |
表二
a | b | c |
6 | 8 | 10 |
8 | 15 | 17 |
10 | 24 | 26 |
12 | 41 |
（1）仔细观察，表一中a为大于1的奇数，此时b、c的数量关系是 ，a、b、c之间的数量关系是 ；
（2）仔细观察，表二中a为大于4的偶数，此时b、c的数量关系是 ，a、b、c之间的数量关系是 ；
（3）我们还发现，表一中的三边长“3，4，5”与表二中的“6，8，10”成倍数关系，表一中的“5，12，13”与表二中的“10，24，26”恰好也成倍数关系……请直接利用这一规律计算：在Rt△ABC中，当
，b=
时，斜边c的值．