题目内容
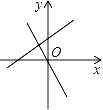
【题目】如图,直线AB:y=kx+2k交x轴于点A,交y轴正半轴于点B,且S△OAB=3
(1) 求A、B两点的坐标
(2) 将直线AB绕A点顺时针旋转45°,交y轴于点C,求直线AC的解析式.

【答案】(1)(-2,0)、(0,3)(2)y=![]()
【解析】
(1)依据直线AB:y=kx+2k交x轴于点A,交y轴正半轴于点B,且S△OAB=3,即可得到A、B两点的坐标;
(2)过点B作BD⊥BA,交AC的延长线于点D,过点D作DH⊥y轴于H.易得△ABO≌△BDH,即可得出D(3,1),设直线AC的解析式为y=ax+b,利用待定系数法即可求得答案.
(1)∵直线AB:y=kx+2k,
令x=0,则y=2k,即B(0,2k),
令y=0,则x=-2,即A(-2,0),
∵S△OAB=3,
∴![]()
∴2k=3,
∴A、B两点的坐标为(-2,0)、(0,3);
(2)如图,过点B作BD⊥BA,交AC的延长线于点D,过点D作DH⊥y轴于H.
∵∠BAC=45°,
∴△ABD是等腰直角三角形,
∴AB=BD,
∵∠AOB=∠BHD=90°,
∴∠ABO=∠BDH,
∴△ABO≌△BDH,
∴DH=BO=3,BH=AO=2,
∴HO=3-2=1,
∴D(3,1),
设直线AC的解析式为y=ax+b,
由A、D两点的坐标可得![]() ,
,
解得:![]() ,
,
∴AC的解析式为:y=![]() .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目