题目内容
 如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于点C,点A、C的坐标分别为(-l,0)、(0,
如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于点C,点A、C的坐标分别为(-l,0)、(0, ),则:
),则:
(1)抛物线对应的函数解析式为______;
(2)若点P为此抛物线上位于x轴上方的一个动点,则△ABP面积的最大值为______.
解:(1)设抛物线y=ax2+bx+ ,
,
∵抛物线的对称轴是直线x=1,
∴- =1,
=1,
即b=-2a,
把点(-l,0)代入得:a-b+ =0,把b=-2a代入
=0,把b=-2a代入
解得:a=- ,b=1,
,b=1,
∴抛物线对应的函数解析式为y=- x2+x+
x2+x+ ;
;
(2)∵A(-1,0),B(3,0),
∴AB=4,
∵y=- x2+x+
x2+x+ ,当x=1时取最大值2,
,当x=1时取最大值2,
∴△ABP面积的最大值为: ×2×4=4.
×2×4=4.
分析:(1)设抛物线y=ax2+bx+ ,根据抛物线的对称轴是直线x=1及过点(-l,0)即可求出a,b的值,从而得出答案;
,根据抛物线的对称轴是直线x=1及过点(-l,0)即可求出a,b的值,从而得出答案;
(2)先求出AB的长,根据P为此抛物线上位于x轴上方的一个动点,求出y的最大值即可求出△ABP面积的最大值.
点评:本题考查了待定系数法求函数解析式及二次函数的性质,属于基础题,关键是掌握用待定系数法求函数解析式及二次函数的性质.
 ,
,∵抛物线的对称轴是直线x=1,
∴-
 =1,
=1,即b=-2a,
把点(-l,0)代入得:a-b+
 =0,把b=-2a代入
=0,把b=-2a代入解得:a=-
 ,b=1,
,b=1,∴抛物线对应的函数解析式为y=-
 x2+x+
x2+x+ ;
;(2)∵A(-1,0),B(3,0),
∴AB=4,
∵y=-
 x2+x+
x2+x+ ,当x=1时取最大值2,
,当x=1时取最大值2,∴△ABP面积的最大值为:
 ×2×4=4.
×2×4=4.分析:(1)设抛物线y=ax2+bx+
 ,根据抛物线的对称轴是直线x=1及过点(-l,0)即可求出a,b的值,从而得出答案;
,根据抛物线的对称轴是直线x=1及过点(-l,0)即可求出a,b的值,从而得出答案;(2)先求出AB的长,根据P为此抛物线上位于x轴上方的一个动点,求出y的最大值即可求出△ABP面积的最大值.
点评:本题考查了待定系数法求函数解析式及二次函数的性质,属于基础题,关键是掌握用待定系数法求函数解析式及二次函数的性质.

练习册系列答案
相关题目
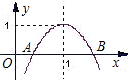 如图,抛物线的对称轴是x=1,与x轴交于A、B两点,若B点的坐标是
如图,抛物线的对称轴是x=1,与x轴交于A、B两点,若B点的坐标是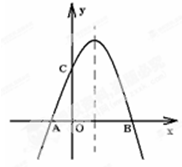 如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点,点A,C的坐标分别为(-1,0),(0,
如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点,点A,C的坐标分别为(-1,0),(0,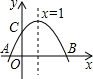 如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于点C,点A、C的坐标分别为(-l,0)、(0,
如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于点C,点A、C的坐标分别为(-l,0)、(0, 如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点.点A、C的坐标分别是(-1,0)、(0,2).
如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点.点A、C的坐标分别是(-1,0)、(0,2). 如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于C点,点A、C的坐标分别是(-1,0)、(0,3)
如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于C点,点A、C的坐标分别是(-1,0)、(0,3)