题目内容
 如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点.点A、C的坐标分别是(-1,0)、(0,2).
如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点.点A、C的坐标分别是(-1,0)、(0,2).(1)求此抛物线对应的函数解析式;
(2)若点P是抛物线上位于x轴上方的一个动点,求△ABP面积的最大值.
(3)试探究:若点Q是抛物线的对称轴x=1上一动点,当点Q在什么位置时△BCQ是等腰三角形.在图中作出符合条件的点Q的位置(保留作图痕迹),并至少求出其中一个点Q的坐标.
分析:(1)根据抛物线的对称性,可根据对称轴解析式和A点坐标求出B点坐标,然后根据A、B、C三点坐标用待定系数法求出抛物线的解析式.
(2)P点在抛物线上方,且三角形ABP面积最大,那么P点纵坐标最大,因此P点即为抛物线的顶点,据此可求出P点坐标,进而可根据三角形的面积公式求出此时三角形ABP的面积.
(3)本题有三种情况:
①QC=QB,此时Q点为线段BC垂直平分线与抛物线对称轴的交点.
②QC=BC,以C为圆心,以BC长为半径作弧,交抛物线对称轴于两点,这两点均符合Q点的条件.
③QB=BC,以B为圆心,BC长为半径作弧,交抛物线对称轴于两点,这两点也都符合Q点的条件.因此综合三种情况共有五个符合条件的Q点,可先设出Q点坐标,然后用坐标系两点间的距离公式表示出BC、BQ、CQ的长,然后根据三种情况中不同的等量关系来求出不同的Q点坐标.
(2)P点在抛物线上方,且三角形ABP面积最大,那么P点纵坐标最大,因此P点即为抛物线的顶点,据此可求出P点坐标,进而可根据三角形的面积公式求出此时三角形ABP的面积.
(3)本题有三种情况:
①QC=QB,此时Q点为线段BC垂直平分线与抛物线对称轴的交点.
②QC=BC,以C为圆心,以BC长为半径作弧,交抛物线对称轴于两点,这两点均符合Q点的条件.
③QB=BC,以B为圆心,BC长为半径作弧,交抛物线对称轴于两点,这两点也都符合Q点的条件.因此综合三种情况共有五个符合条件的Q点,可先设出Q点坐标,然后用坐标系两点间的距离公式表示出BC、BQ、CQ的长,然后根据三种情况中不同的等量关系来求出不同的Q点坐标.
解答: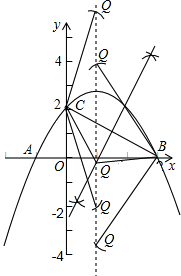 解:(1)∵抛物线的对称轴为x=1,且A(-1,0);
解:(1)∵抛物线的对称轴为x=1,且A(-1,0);
∴B(3,0);
设抛物线的解析式为y=a(x+1)(x-3);
已知抛物线过C(0,2),则有:
2=a(0+1)(0-3),
即a=-
∴函数解析式y=-
(x+1)(x-3)=-
(x-1)2+
;
(2)当△ABP面积最大,且P在x轴上方时,此时P点为抛物线顶点.
由(1)知:P(1,
).
∴Smax=
AB•yP=
×4×
=
.
(3)点Q共有五个,其中一个点Q的坐标如:Q(1,2+2
).
 解:(1)∵抛物线的对称轴为x=1,且A(-1,0);
解:(1)∵抛物线的对称轴为x=1,且A(-1,0);∴B(3,0);
设抛物线的解析式为y=a(x+1)(x-3);
已知抛物线过C(0,2),则有:
2=a(0+1)(0-3),
即a=-
| 2 |
| 3 |
∴函数解析式y=-
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
(2)当△ABP面积最大,且P在x轴上方时,此时P点为抛物线顶点.
由(1)知:P(1,
| 8 |
| 3 |
∴Smax=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 16 |
| 3 |
(3)点Q共有五个,其中一个点Q的坐标如:Q(1,2+2
| 3 |
点评:本题考查了二次函数解析式的确定、图形面积的求法、等腰三角形的判定等知识.要注意(3)题中要将所有的情况都考虑到.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
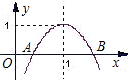 如图,抛物线的对称轴是x=1,与x轴交于A、B两点,若B点的坐标是
如图,抛物线的对称轴是x=1,与x轴交于A、B两点,若B点的坐标是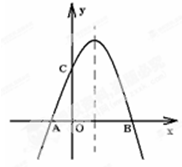 如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点,点A,C的坐标分别为(-1,0),(0,
如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点,点A,C的坐标分别为(-1,0),(0,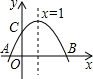 如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于点C,点A、C的坐标分别为(-l,0)、(0,
如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于点C,点A、C的坐标分别为(-l,0)、(0, 如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于C点,点A、C的坐标分别是(-1,0)、(0,3)
如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于C点,点A、C的坐标分别是(-1,0)、(0,3)