题目内容
直线y=-2x经过点P（-2，a），点P关于y轴的对称点P′，则点P′的坐标是
（2，4）
（2，4）
．分析：将点P（-2，a）代入直线y=-2x得到a的值，从而求出P的坐标，再根据关于y轴对称的点的坐标特征，求出点P′的坐标．
解答：解：将点P（-2，a）代入直线y=-2x得，
a=-2×（-2）=4，
则P点坐标为（-2，4），
由于点P关于y轴的对称点P′，
则P′坐标为（2，4）．
故答案为（2，4）．
a=-2×（-2）=4，
则P点坐标为（-2，4），
由于点P关于y轴的对称点P′，
则P′坐标为（2，4）．
故答案为（2，4）．
点评：本题考查了一次函数图象上点的坐标特征，经过函数的某点一定在函数的图象上，且关于y轴对称的点的纵坐标相同，横坐标互为相反数．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
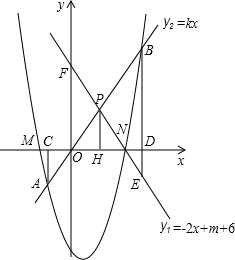两侧，点N在点M的右边，直线y1=-2x+m+6经过点N，交y轴于点F．