��Ŀ����
��֪����ͼ��������y=x2-��m+2��x+3��m-1����x�����������M��N��ԭ���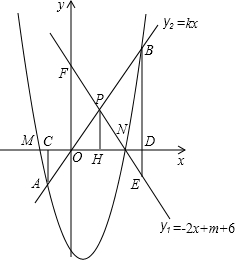 ���࣬��N�ڵ�M���ұߣ�ֱ��y1=-2x+m+6������N����y���ڵ�F��
���࣬��N�ڵ�M���ұߣ�ֱ��y1=-2x+m+6������N����y���ڵ�F����1�������������ߺ�ֱ�ߵĽ���ʽ��
��2����ֱ��y2=kx��k��0���������߽���������ͬ�ĵ�A��B����ֱ��y1���ڵ�P���ֱ����A��B��P��x��Ĵ��ߣ�����ֱ���C��D��H��
�����ú���k�Ĵ���ʽ��ʾ
| 1 |
| OC |
| 1 |
| OD |
����֤��
| 1 |
| OC |
| 1 |
| OD |
| 2 |
| OH |
��3���ڣ�2���������£��ӳ��߶�BD��ֱ��y1�ڵ�E����ֱ��y2�Ƶ�O��תʱ�����Ƿ��������������kֵ��ʹ��PBEΪ���������Σ������ڣ����ֱ��y2�Ľ���ʽ���������ڣ���˵�����ɣ�
��������1�����ȸ���ֱ��y1�Ľ���ʽ���N������꣬Ȼ������������ߵĽ���ʽ�м������m��ֵ��Ȼ�����M��N��ԭ�����࣬��3��m-1����0�������������m��ֵ��ȥ��������������ߺ�ֱ�ߵĽ���ʽ��
��2��������������ཻ�����Ľ���ʽ�����C��D��H����ĺ����꣬Ȼ���ø���ϵ���Ĺ�ϵ������⼴�ɣ�
��3������Ҫ����������������ۣ�
�ٵ�PB=BEʱ�����С�OFD=��OF�����ڡ�OFDΪ�����С��45�㣬��ˡ�FOBΪ�۽ǣ���ʱֱ��y2��б��k��0����Ȼ�������⣮
�ڵ�PB=PEʱ����ôPF=PO��P��λ��OF�Ĵ�ֱƽ�����ϣ����P���������Ϊ3���ɴ˿����P������꣮�Դ������ֱ��y2�Ľ���ʽ��
�۵�PE=BEʱ����ôPF=OF=6���ɹ�P��PG��y����G��ͨ���������������������P��ĺ����꣬��������ֱ��y1�Ľ���ʽ���P������꣬�Դ������ֱ��y2�Ľ���ʽ��
��������������÷���������ֱ��y2�Ľ���ʽ��
��2��������������ཻ�����Ľ���ʽ�����C��D��H����ĺ����꣬Ȼ���ø���ϵ���Ĺ�ϵ������⼴�ɣ�
��3������Ҫ����������������ۣ�
�ٵ�PB=BEʱ�����С�OFD=��OF�����ڡ�OFDΪ�����С��45�㣬��ˡ�FOBΪ�۽ǣ���ʱֱ��y2��б��k��0����Ȼ�������⣮
�ڵ�PB=PEʱ����ôPF=PO��P��λ��OF�Ĵ�ֱƽ�����ϣ����P���������Ϊ3���ɴ˿����P������꣮�Դ������ֱ��y2�Ľ���ʽ��
�۵�PE=BEʱ����ôPF=OF=6���ɹ�P��PG��y����G��ͨ���������������������P��ĺ����꣬��������ֱ��y1�Ľ���ʽ���P������꣬�Դ������ֱ��y2�Ľ���ʽ��
��������������÷���������ֱ��y2�Ľ���ʽ��
����⣺��1���������֪��N�������Ϊ��
��0����
��֪�����߹�N�㣬���У�
-
+3��m-1��+0
��m2-8m=0�����m=0��m=8��
��M��N��ԭ�����࣬���3��m-1����0��m��1��
���m=8����������ȥ
��m=0��
�������ߵĽ���ʽΪy=x2-2x-3��ֱ�ߵĽ���ʽΪy1=-2x+6��
��2����֪��������ֱ��y2����A��B���㣬
���kx=x2-2x+3��
��x2-��2+k��x-3=0
��C��D��������x1��0������x2��0����
��x1+x2=2+k��x1•x2=-3
��
-
=
=
=
��
��ֱ֪��y2��y1����P�㣬
��-2x+6=kx��x=
��H���������
��0��
���
=
��
��
-
=
��
��3������Ҫ�����������
��PB=BE������OFD=��OPF��
�ߡ�OFD��45�㣬
���FOBΪ�۽ǣ���ʱy2��б��k��0��
��˲������⣬���������������
��PB=PE������PF=PO����P���������x��y����
��y=
OF=3��
��ֱ֪��y1��P�㣬
���P���������
��3����
��3=
k��k=2��
���ֱ��y2�Ľ���ʽΪy2=2x��
��PE=BE������PF=OF=6����P��PG��y����G�����P��������x��y����
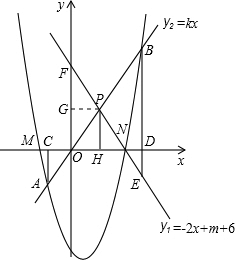 ��ֱ��������OEF�У�OE=3��OF=6��
��ֱ��������OEF�У�OE=3��OF=6��
���ݹ��ɶ����ɵã�EF=3
��
��PG��x��
��
=
��
��
=
��
��x=
��
����ֱ��y1=-2x+6��P�㣬
���P���������
��
����
��
=k•
��k=
-2��
��y2=��
-2��x��
��������y2�Ľ���ʽΪy2=2x��y2=��
-2��x��
| m+6 |
| 2 |
��֪�����߹�N�㣬���У�
| (m+6)2 |
| 4 |
| (m+6)(m+2) |
| 2 |
��m2-8m=0�����m=0��m=8��
��M��N��ԭ�����࣬���3��m-1����0��m��1��
���m=8����������ȥ
��m=0��
�������ߵĽ���ʽΪy=x2-2x-3��ֱ�ߵĽ���ʽΪy1=-2x+6��
��2����֪��������ֱ��y2����A��B���㣬
���kx=x2-2x+3��
��x2-��2+k��x-3=0
��C��D��������x1��0������x2��0����
��x1+x2=2+k��x1•x2=-3
��
| 1 |
| OC |
| 1 |
| OD |
| OD-OC |
| OC•OD |
| x1+x2 |
| -x1x2 |
| 2+k |
| 3 |
��ֱ֪��y2��y1����P�㣬
��-2x+6=kx��x=
| 6 |
| k+2 |
��H���������
| 6 |
| k+2 |
���
| 2 |
| OH |
| 2+k |
| 3 |
��
| 1 |
| OC |
| 1 |
| OD |
| 2 |
| OH |
��3������Ҫ�����������
��PB=BE������OFD=��OPF��
�ߡ�OFD��45�㣬
���FOBΪ�۽ǣ���ʱy2��б��k��0��
��˲������⣬���������������
��PB=PE������PF=PO����P���������x��y����
��y=
| 1 |
| 2 |
��ֱ֪��y1��P�㣬
���P���������
| 3 |
| 2 |
��3=
| 3 |
| 2 |
���ֱ��y2�Ľ���ʽΪy2=2x��
��PE=BE������PF=OF=6����P��PG��y����G�����P��������x��y����
 ��ֱ��������OEF�У�OE=3��OF=6��
��ֱ��������OEF�У�OE=3��OF=6�����ݹ��ɶ����ɵã�EF=3
| 5 |
��PG��x��
��
| PF |
| NF |
| PG |
| ON |
��
| 6 | ||
3
|
| x |
| 3 |
��x=
6
| ||
| 5 |
����ֱ��y1=-2x+6��P�㣬
���P���������
6
| ||
| 5 |
30-12
| ||
| 5 |
��
30-12
| ||
| 5 |
6
| ||
| 5 |
| 5 |
��y2=��
| 5 |
��������y2�Ľ���ʽΪy2=2x��y2=��
| 5 |
���������⿼����һ�κ����Ͷ��κ�������ʽ��ȷ�������κ�����һԪ���η��̵Ĺ�ϵ��һԪ���η��̸���ϵ���Ĺ�ϵ������ͼ��Ľ��㡢���������εĹ��������֪ʶ�㣬�ۺ���ǿ����Ҫ����ѧ���������ۡ����ν�ϵ���ѧ˼�뷽����

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
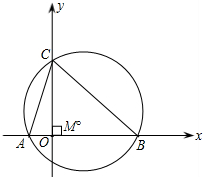 ��y�ύ��C��������Ϊ3����ABC�����Բ��Բ��Ϊ��M��
��y�ύ��C��������Ϊ3����ABC�����Բ��Բ��Ϊ��M�� ���������ϣ��������Ϊ12��
���������ϣ��������Ϊ12�� ��2013•�������ʼ죩��֪����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A��
��2013•�������ʼ죩��֪����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A�� ��֪����ͼ��������y=ax2-2ax+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0����
��֪����ͼ��������y=ax2-2ax+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0���� ��֪����ͼ��������y=x2+px+q��x���ཻ��A��B���㣬��y�ύ�ڵ�C����OA��OB��OA=OC���������ߵĶ���Ϊ��P��ֱ��PC��x��Ľ���Dǡ�����A����y��Գƣ�
��֪����ͼ��������y=x2+px+q��x���ཻ��A��B���㣬��y�ύ�ڵ�C����OA��OB��OA=OC���������ߵĶ���Ϊ��P��ֱ��PC��x��Ľ���Dǡ�����A����y��Գƣ�