题目内容
【题目】(1)引入:
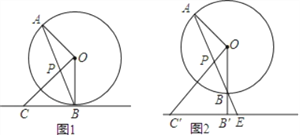
如图1,直线AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC,直线BC是否与⊙O相切,为什么?
(2)引申:
如图2,记(1)中⊙O的切线为直线l,在(1)的条件下,将切线l向下平移,设平移后的直线l与OB的延长线相交于点B′,与AB的延长线相交于点E,与OP的延长线相交于点C′,找出图2中与C′P相等的线段,并说明理由.
【答案】(1)相切,(2)C′P=C′E.
【解析】试题分析:(1)由OC⊥OA,易得∠APO+∠OAB=90°,然后由等腰三角形的性质可得∠OAB=∠ABO,∠CBP=∠CPB,等量代换可得∠CBP+∠OBA=90°,即∠OBC-90°,由切线的判定可得出结论;
(2)由(1)可得∠OAB+∠C′PE=90°,等量代换可得∠ABO+∠C′PE=90°,由∠EBB′+∠BEB′=90°,∠EBB′=∠ABO,易得∠C′PE=∠BEB′,得出结论.
试题解析:(1)相切,
∵OC⊥OA,
∴∠AOC=90°,
∴∠APO+∠OAB=90°,
∵OA=OB,
∴∠OAB=∠ABO,
∵PC=PB,
∴∠CBP=∠CPB,
∵∠APO=∠CPB,
∴∠CBP+∠OBA=90°,
即∠OBC=90°,
∴OB⊥BC
∵OB为半径,
∴BC与⊙O相切;
(2)C′P=C′E,
∵∠OB′C′=90°,∠APO+∠OAB=90°,且∠APO=∠C′PE,
∴∠OAB+∠C′PE=90°,
∵OA=OB,
∴∠OAB=∠ABO,
∴∠ABO+∠C′PE=90°,
∵∠EBB′+∠BEB′=90°,且∠EBB′=∠ABO,
∴∠C′PE=∠BEB′,
∴C′P=C′E.

【题目】某鞋店销售一款新式女鞋,试销期间对该款不同型号的女鞋销售量统计如下表:
尺码/厘米 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
销售量/双 | 1 | 2 | 3 | 11 | 8 | 6 | 4 |
该店经理如果想要了解哪种女鞋的销售量最大,那么他应关注的统计量是_____.