题目内容
已知M(a,b)是平面直角坐标系xOy中的点,其中a是从l,2,3,4三个数中任取的一个数,b是从l,2,3,4,5五个数中任取的一个数.定义“点M(a,b)在直线x+y=n上”为事件Qn(2≤n≤9,n为整数),则当Qn的概率最大时,n的所有可能的值为( )
| A、5 | B、4或5 | C、5或6 | D、6或7 |
分析:利用树状图列举出所有可能,即可得出n的值,进而得出答案.
解答:解:
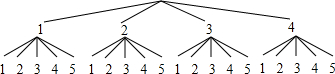
∵a是从l,2,3,4四个数中任取的一个数,b是从l,2,3,4,5五个数中任取的一个数.
又∵点M(a,b)在直线x+y=n上,2≤n≤9,n为整数,
∴n=5或6的概率是
,n=4的概率是
,
∴当Qn的概率最大时是n=5或6的概率是
最大.
故选C.

∵a是从l,2,3,4四个数中任取的一个数,b是从l,2,3,4,5五个数中任取的一个数.
又∵点M(a,b)在直线x+y=n上,2≤n≤9,n为整数,
∴n=5或6的概率是
| 1 |
| 4 |
| 3 |
| 16 |
∴当Qn的概率最大时是n=5或6的概率是
| 1 |
| 4 |
故选C.
点评:此题主要考查了树状图法求概率,利用树状图法列举出所有可能是解决问题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目



