题目内容
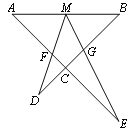
【题目】如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,
且DM交AC于F,ME交BC于G.
(1)写出图中三对相似三角形,并证明其中的一对;
(2)连结FG,如果α=45°,AB=![]() ,AF=3,求FG的长.
,AF=3,求FG的长.
【答案】(1)△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM(写出两对即可)(2)![]()
【解析】试题分析:(1)根据已知条件,∠DME=∠A=∠B=α,结合图形上的公共角,即可推出△DMG∽△DBM,△EMF∽△EAM,AMF∽△BGM;
(2)根据相似三角形的性质,推出BG的长度,依据锐角三角函数推出AC的长度,即可求出CG、CF的长度,继而推出FG的长度.
试题解析:(1)△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM(写出两对即可)
以下证明△AMF∽△BGM.
∵∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B
∴△AMF∽△BGM.
(2)连接FG,

当α=45°时,可得AC⊥BC且AC=BC
∵M为AB的中点,
∴AM=BM=![]()
又∵AMF∽△BGM,
∴![]()
∴![]()
又![]() ,
,
∴![]() ,
, ![]()
∴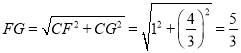

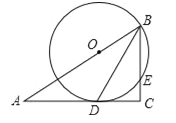
【题目】如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
【题目】为迎接“五一”节的到来,某食品连锁店对某种商品进行了跟踪调查,发现每天它的销售价与销售量之间有如下关系:
每千克售价(元) | 25 | 24 | 23 | … | 15 |
每天销售量(千克) | 30 | 32 | 34 | … | 50 |
如果单价从最高25元/千克下调到x元/千克时,销售量为y千克,已知y与x之间的函数关系是一次函数:
(1)求y与x之间的函数解析式;(不写定义域)
(2)若该种商品成本价是15元/千克,为使“五一”节这天该商品的销售总利润是200元,那么这一天每千克的销售价应定为多少元?
