题目内容
在梯形ABCD中,如果有两个内角是70°,那么梯形ABCD是等腰梯形吗?请说明理由.(提示:解决问题时可借助图形进行说理)
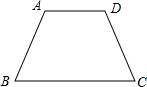 解:在梯形ABCD中,如果有两个内角是70°,那么梯形ABCD是等腰梯形.
解:在梯形ABCD中,如果有两个内角是70°,那么梯形ABCD是等腰梯形.理由:如图,在梯形ABCD中,设AD∥BC,AD<BC,
(1)当∠B=∠A=70°时,∠A+∠B=140°,
∵AD∥BC,
∴∠A+∠B=180°,矛盾,
∴这种情况不成立;
(2)当∠B=∠D=70°时,
∵AD∥BC,
∴∠A+∠B=180°,∠C+∠D=180°,
∴∠A=∠C,
∴四边形ABCD是平行四边形,AD=BC,矛盾,
∴这种情况不成立;
(3)当∠B=∠C=70°时,∠B+∠C=140°,
∴AB与CD不平行,
∵AD∥BC,
∴此时四边形ABCD是等腰梯形.
综上所述,在梯形ABCD中,如果有两个内角是70°,那么梯形ABCD是等腰梯形.
分析:首先根据题意画出图形,然后分别从∠B=∠A=70°,∠B=∠D=70°以及∠B=∠C=70°去分析求解即可求得答案.
点评:此题考查了梯形的性质、等腰梯形的判定以及平行四边形的性质.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
相关题目
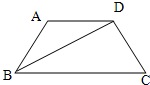 13、如图,在梯形ABCD中,AB=AD=CD,∠DBC=25°,则∠BDC=
13、如图,在梯形ABCD中,AB=AD=CD,∠DBC=25°,则∠BDC=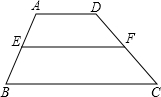 在梯形ABCD中,如图所示,AD∥BC,点E、F分别是AB、CD的中点,连接EF,EF叫做梯形的中位线.观察EF的位置,联想三角形的中位线定理,请你猜想:EF与AD、BC有怎样的位置和数量关系并证明你的猜想.
在梯形ABCD中,如图所示,AD∥BC,点E、F分别是AB、CD的中点,连接EF,EF叫做梯形的中位线.观察EF的位置,联想三角形的中位线定理,请你猜想:EF与AD、BC有怎样的位置和数量关系并证明你的猜想. 如图所示,在梯形ABCD中,AB∥CD,AD=BC=DC,且∠A=60°.
如图所示,在梯形ABCD中,AB∥CD,AD=BC=DC,且∠A=60°.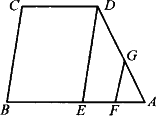
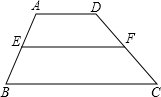 在梯形ABCD中,如图所示,AD∥BC,点E、F分别是AB、CD的中点,连接EF,EF叫做梯形的中位线.观察EF的位置,联想三角形的中位线定理,请你猜想:EF与AD、BC有怎样的位置和数量关系并证明你的猜想.
在梯形ABCD中,如图所示,AD∥BC,点E、F分别是AB、CD的中点,连接EF,EF叫做梯形的中位线.观察EF的位置,联想三角形的中位线定理,请你猜想:EF与AD、BC有怎样的位置和数量关系并证明你的猜想.