题目内容
若直线y=-2x-4与直线y=4x+b的交点在第三象限,则b的取值范围是( )A.-4<b<8
B.-4<b<0
C.b<-4或b>8
D.-4≤b≤8
【答案】分析:首先把y=-2x-4和y=4x+b,组成方程组,求解,x和y的值都用b来表示,再根据交点坐标在第三象限表明x、y都小于0,即可求得b的取值范围.
解答:解: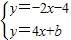 ,
,
解得: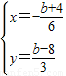 ,
,
∵交点在第三象限,
∴- <0,
<0,
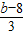 <0,
<0,
解得:b>-4,b<8,
∴-4<b<8.
故选:A.
点评:本题主要考查两直线相交的问题,关键在于解方程组用含b的式子表示x、y,根据在第三象限的点坐标性质解不等式即可.
解答:解:
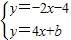 ,
,解得:
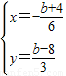 ,
,∵交点在第三象限,
∴-
 <0,
<0,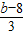 <0,
<0,解得:b>-4,b<8,
∴-4<b<8.
故选:A.
点评:本题主要考查两直线相交的问题,关键在于解方程组用含b的式子表示x、y,根据在第三象限的点坐标性质解不等式即可.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目