题目内容
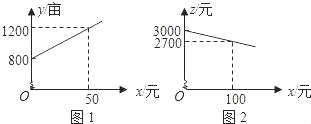
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植-亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.
【答案】(1)2400000元;(2)种植亩数与政府补贴的函数关系为:y=8x+800;每亩蔬菜的收益与政府补贴的函数关系为z=-3x+3000(x>0);(3)政府每亩补贴450元时,总收益额最大,为7260000元.
【解析】
试题分析:(1)根据题意可知直接计算这种蔬菜的收益额为3000×800=2400000(元);
(2)设种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式分别为:y=kx+800,z=k1x+3000,并根据图象上点的坐标利用待定系数法求函数的解析式即可;
(3)表示出蔬菜的总收益w(元)与x之间的关系式,w=-24x2+21600x+2400000,利用二次函数最值问题求最大值.
试题解析:(1)政府没出台补贴政策前,这种蔬菜的收益额为3000×800=2400000(元)
(2)设种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式分别为:
y=kx+800,z=k1x+3000,
分别把点(50,1200),(100,2700)代入得,
50k+800=1200,100k1+3000=2700,
解得:k=8,k1=-3,
种植亩数与政府补贴的函数关系为:y=8x+800
每亩蔬菜的收益与政府补贴的函数关系为z=-3x+3000(x>0)
(3)由题意:
w=yz=(8x+800)(-3x+3000)
=-24x2+21600x+2400000
=-24(x-450)2+7260000,
∴当x=450,即政府每亩补贴450元时,总收益额最大,为7260000元.

 发散思维新课堂系列答案
发散思维新课堂系列答案