题目内容
(2010•西宁)如图,在△ABC中,AD⊥BC,垂足为D.(1)尺规作图(不写作法,保留作图痕迹):作△ABC的外接圆⊙O,作直径AE,连接BE;
(2)若AB=8,AC=6,AD=5,求直径AE的长.(证明△ABE∽△ADC)

【答案】分析:(1)由于三角形的外心是三边中垂线的交点,可作△ABC任意两边的垂直平分线,它们的交点即为外接圆的圆心O,确定了圆心即可画出⊙O及直径AE.
(2)由圆周角定理可得:∠C=∠E,∠ABE=∠ADC=90°,由此可证得△ADC∽△ABE,根据所得比例线段即可求得直径AE的长.
解答: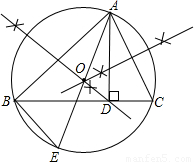 解:(1)正确作出△ABC的外接圆⊙O,(3分)
解:(1)正确作出△ABC的外接圆⊙O,(3分)
正确作出直径AE;(4分)
(2)证明:由作图可知AE为⊙O的直径,
∴∠ABE=90°,(直径所对的圆周角是直角)
∵AD⊥BC,
∴∠ADC=90°,
∴∠ABE=∠ADC,
∵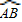 =
= ,
,
∴∠E=∠C,
∴△ABE∽△ADC,(8分)
∴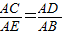 ,即
,即 ,
,
∴AE=9.6.
点评:解决此题的关键是熟练掌握三角形外心的定义,要熟记此题的作图方法,这在求三角形的外接圆半径(或直径)时,是常用也是主要的辅助线作法.
(2)由圆周角定理可得:∠C=∠E,∠ABE=∠ADC=90°,由此可证得△ADC∽△ABE,根据所得比例线段即可求得直径AE的长.
解答:
 解:(1)正确作出△ABC的外接圆⊙O,(3分)
解:(1)正确作出△ABC的外接圆⊙O,(3分)正确作出直径AE;(4分)
(2)证明:由作图可知AE为⊙O的直径,
∴∠ABE=90°,(直径所对的圆周角是直角)
∵AD⊥BC,
∴∠ADC=90°,
∴∠ABE=∠ADC,
∵
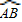 =
= ,
,∴∠E=∠C,
∴△ABE∽△ADC,(8分)
∴
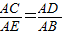 ,即
,即 ,
,∴AE=9.6.
点评:解决此题的关键是熟练掌握三角形外心的定义,要熟记此题的作图方法,这在求三角形的外接圆半径(或直径)时,是常用也是主要的辅助线作法.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目



