题目内容
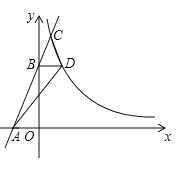
【题目】如图,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8m,PD=2m,CF=1m,∠DPE=15°.根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳,在上午10:00时,太阳光线与地面的夹角为65°,若要遮阳效果最佳AP的长约为( )
(参考数据:sin65°≈0.91,cos65°≈0.42,sin50°≈0.77,cos50°≈0.64)

A.1.2mB.1.3mC.1.5mD.2.0m
【答案】C
【解析】
过点F作FG⊥AC于点G,根据题意可得,当太阳光线与PE垂直时,遮阳效果最佳,即∠BEP=90°,再根据四边形内角和定理可得∠CPF的度数,再根据锐角三角函数即可求出CP的长,进而可得遮阳效果最佳时AP的长.
如图,过点F作FG⊥AC于点G,
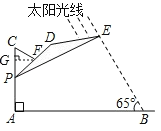
根据题意可知:
当太阳光线与PE垂直时,遮阳效果最佳,
∴∠BEP=90°.
∵∠A=90°,∠B=65°,
∴∠EPA=360°﹣90°﹣90°﹣65°=115°.
∵∠DPE=15°,
∴∠APD=130°,
∴∠CPF=50°.
∵F为PD的中点,
∴DF=PF![]() PD=1,
PD=1,
∴CF=PF=1,
∴CP=2PG=2×PFcos50°≈2×1×0.64≈1.28,
∴AP=AC﹣PC=2.8﹣1.28≈1.5(m).
所以要遮阳效果最佳AP的长约为1.5米.
故选:C.

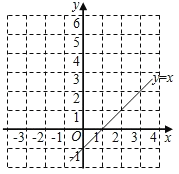
【题目】已知函数y![]() ,请根据已学知识探究该函数的图象和性质.
,请根据已学知识探究该函数的图象和性质.
(1)列表,写出表中a、b,c的值:a= ,b= ,c= ;
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0.5 | a | 2.5 | b | 2.5 | 1 | c | … |
(2)描点,连线:在如图的平面直角坐标系中画出该函数的图象,并写出该函数的一条性质: ;
(3)已知函数y=x﹣1的图象如图所示,结合你所画的函数图象,直接写出不等式![]() x﹣1的解集: .
x﹣1的解集: .